Reale und ideale Kreisprozesse

Wärmekraftmaschinen – wie beispielsweise Dampfmaschinen oder Ottomotoren – verrichten nach Wärmezufuhr mechanische Arbeit. Eine solche Maschine soll natürlich nicht nur einmalig, sondern kontinuierlich laufen können. Es muss also am Ende eines Arbeitsganges wieder der Ausgangszustand herrschen, damit der nächste Arbeitsgang nahtlos anschließen kann. Das heißt, die Maschine muss einen periodischen Prozess durchlaufen, den man als Kreisprozess bezeichnet.

  Abb. 2 ¦ Prinzip des Otto-Motors  

Bildunterschrift1. Takt – Ansaugtakt: Im Vergaser wird ein Benzin-Luft-Gemisch erzeugt und durch den nach unten gehenden Kolben in den Zylinder gesaugt.
2. Takt – Verdichtungstakt: Das Benzin-Luft-Gemisch wird durch den Kolben verdichtet.
3. Takt – Arbeitstakt Von der Zündkerze erzeugte elektrische Funken entzünden das Gemisch. Es verbrennt, dehnt sich aus und bewegt den Kolben nach unten.
4. Takt – Auspufftakt: Der sich wieder nach oben bewegende Kolben drückt die Abgase durch das Auslassventil hinaus.Bildunterschrift Ende

Nun wissen wir aus dem zweiten Hauptsatz der Thermodynamik, dass die Wärme nicht vollständig als Arbeit genutzt werden kann, sondern immer ein Teil ungenutzt verloren geht – und zwar auch dann, wenn es keine Verluste durch Reibung oder Strahlung gibt, es sich also um einen idealen Kreisprozess handelt. Ein solcher idealer Kreisprozess ist der so genannte carnotsche Kreisprozess (nach seinem Erfinder S. Carnot). „Ideal“ deshalb, weil in ihm nur mit idealen Gasen gearbeitet wird und keine Reibungsverluste auftreten. Ein ideales Gas liegt immer gasförmig vor, es kondensiert nicht. Sowohl Reibung als auch Kondensieren sind Effekte, die eine Wechselwirkung zwischen den Teilchen eines Gases untereinander und mit den Teilchen der Wände voraussetzen. Die Teilchen idealer Gase wechselwirken aber definitionsgemäß nicht. (Reale Gase verhalten sich daher nur unter bestimmten Bedingungen wie genügend hoher Temperatur und genügend geringem Druck wie ideale Gase.)

Der carnotsche Kreisprozess ist ein reversibler Kreisprozess – weshalb er in der Realität nicht herstellbar ist. Er besteht aus je zwei isothermen und adiabatischen Teilprozessen. „Isotherm“ bedeutet, dass sich die Temperatur des Systems nicht ändert, hier also die Temperatur des Gases. Damit bleibt beim idealen Gas auch die innere Energie konstant, da diese beim idealen Gas nur von der Temperatur des Gases abhängt. „Adiabatisch“ heißt ein Prozess dann, wenn kein Wärmeaustausch mit der Umgebung (oder den Wärmespeichern) möglich ist. Vom Gas verrichtete Arbeit hat beim adiabatischen Prozess daher eine Abnahme der inneren Energie des Gases zur Folge, am Gas verrichtete Arbeit erhöht die innere Energie des Gases. (Die innere Energie eines Gases kann durch Arbeitsverrichtung und Wärmeaustausch geändert werden. Da Wärmeaustausch im adiabatischen Fall ausgeschlossen ist, entspricht die Änderung der inneren Energie genau der Arbeitsleistung.)

Versuchsaufbau zum carnotschen Kreisprozess

  Abb. 1 ¦ Der carnotsche Kreisprozess  

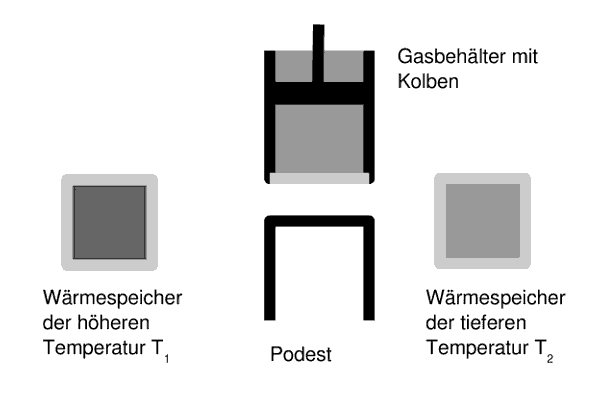
BildunterschriftDie schwarzen Linien stellen absolut wärmeundurchlässige Wände dar; die hellgrauen sind völlig durchlässig für Wärme.Bildunterschrift Ende

Die einzelnen Schritte im carnotschen Kreisprozess

Im carnotschen Kreisprozess wechseln isotherme und adiabatische Schritte einander ab. Insgesamt wird zweimal Arbeit hineingesteckt und zweimal Arbeit herausgeholt; einmal geht Wärme Q₁ auf das Gas über, einmal die kleinere Menge Wärme Q₂ auf den kälteren Wärmespeicher. Man kann nun ausrechnen, dass netto eine Arbeit A vom System verrichtet wird (also aus dem System gewonnen wird), die der Differenz von aufgenommenem und abgegebenem Wärmebetrag entspricht: A = Q₁ − Q₂. Oder auch anders formuliert: Die aufgenommene Wärme Q₁ ist die Summe aus der verrichteten Arbeit und der wieder abgegebenen Wärme Q₂. Es wird also nicht die ganze aufgenommene Wärme in Arbeit umgewandelt.

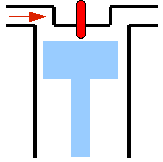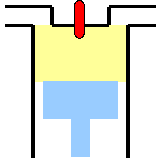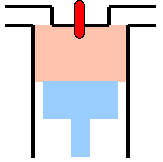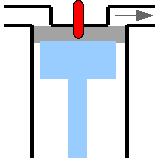
  Abb. 3 ¦ Die einzelnen Schritte im carnotschen Kreisprozess  

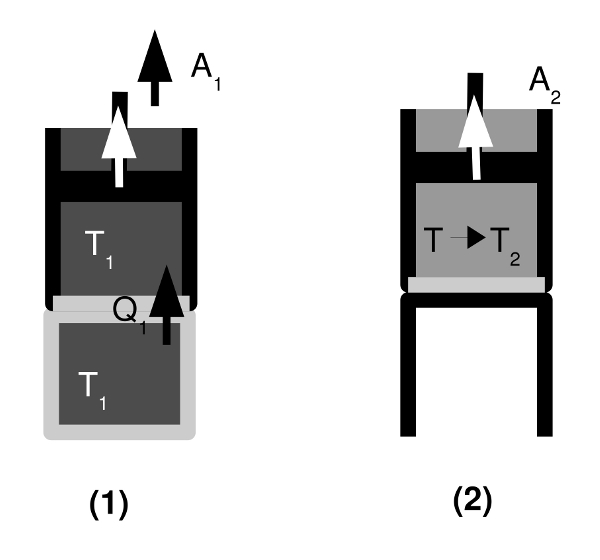
Bildunterschrift(1) Isotherme Expansion
Das Gas im Gasbehälter hat zu Beginn die höhere Temperatur T₁. Der Gasbehälter mit dem Kolben wird in Kontakt mit dem Wärmespeicher der höheren Temperatur gebracht. Das Gas der Temperatur T₁ dehnt sich aus und bewegt den Kolben, verrichtet also die Arbeit A₁. Vom Wärmespeicher der höheren Temperatur T₁ wird die Wärme Q₁ auf das Gas übertragen und gleicht die Abnahme von Temperatur und innerer Energie im Gas sofort aus. Die Temperatur des Gases T₁ ändert sich daher nicht und ist gleich der des Wärmespeichers.

(2) Adiabatische Expansion
Der Gasbehälter wird auf ein wärmeisolierendes Podest gesetzt. Das Podest isoliert die Unterseite des Gasbehälters gegen Wärmeaustausch – es findet somit jetzt keine Wärmezufuhr mehr statt. Das Gas expandiert weiter, es verrichtet die Arbeit A₂ am Kolben, seine innere Energie nimmt nun aber ab (da keine Wärme zum Ausgleich mehr zugeführt wird), bis es die Temperatur T₂ des kälteren Wärmespeichers erreicht hat.Bildunterschrift Ende

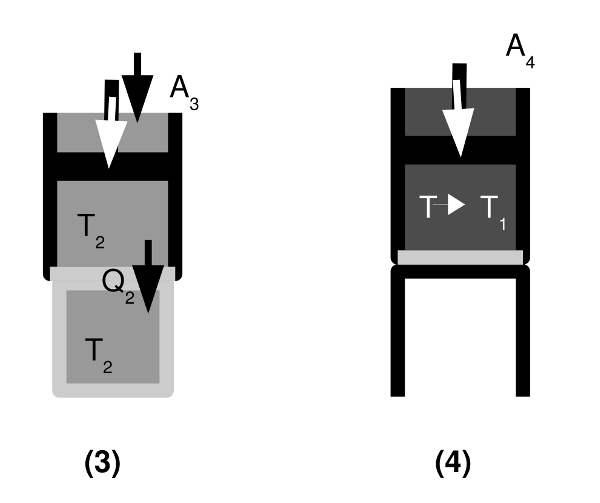
Bildunterschrift(3) Isotherme Kompression
Das Gas im Gasbehälter hat die nun niedrigere Temperatur T₂. Der Gasbehälter mit dem Kolben wird in Kontakt mit dem Wärmespeicher der niedrigeren Temperatur gebracht. Das Gas wird durch den Kolben komprimiert, es wird also die Arbeit A₃ an ihm verrichtet. Vom Gas wird die Wärme Q₂ auf den Wärmespeicher der niedrigeren Temperatur T₂ übertragen; die Zunahme der Temperatur und damit der inneren Energie wird also sofort ausgeglichen. Die Temperatur T₂ des Gases ändert sich daher nicht und bleibt gleich der des kälteren Wärmespeichers.

(4) Adiabatische Kompression
Der Gasbehälter wird wieder auf das wärmeisolierende Podest gesetzt. Das Podest isoliert die Unterseite des Gasbehälters gegen Wärmeaustausch – es findet somit jetzt keine Wärmeabgabe mehr statt. Das Gas wird weiter komprimiert, die Arbeit A₄ an ihm verrichtet – seine innere Energie nimmt zu, bis seine Temperatur wieder gleich der Temperatur T₁ des wärmeren Wärmespeichers ist.
Danach kann es mit Schritt 1 von vorn losgehen.Bildunterschrift Ende

Wirkungsgrad

Im 2. Schritt verrichtet das Gas Arbeit, im 4. Schritt wird Arbeit am Gas verrichtet (siehe Abbildung 2). Insgesamt wird beim carnotschen Kreisprozess jedoch vom Gas Arbeit verrichtet – man gewinnt also Arbeit. Diese gewonnene Arbeit ergibt sich als Differenz aus der im 1. Schritt aufgenommenen Wärme und der im 3. Schritt abgegebenen Wärme. Wird der carnotsche Kreisprozess einmal vollständig durchlaufen, hat das System seinen Anfangszustand exakt wieder erreicht, denn da es ein reversibler Prozess ist, ist „unterwegs“ keine Reibungswärme verloren gegangen. Für reversible Prozesse ist die Entropieänderung null. Es gilt also, dass die Entropieänderung für die Wärmeaufnahme bei der höheren Temperatur (Schritt 1) und die Entropieänderung für die Wärmeabgabe bei der niedrigeren Temperatur (Schritt 3) zusammen null ergeben. Diese Gleichung erlaubt es, zusammen mit der Formel für die gewonnene Arbeit den Wirkungsgrad zu berechnen. Der Wirkungsgrad gibt an, wie viel von der aufgenommenen Wärme in nutzbare Arbeit umgewandelt werden kann. Für den carnotschen Kreisprozess ergibt sich: η = 1 − T₂ / T₁, wobei T₁ die höhere Temperatur ist, auf die das Gas erhitzt wird, und T₂ die niedrigere, auf die das Gas am Ende des Kreisprozesses abgekühlt wird. Wie man sieht, ist der Wirkungsgrad kleiner als 1. Auch das ist wieder eine Auswirkung des zweiten Hauptsatzes der Thermodynamik. Da T₁ die höhere Temperatur ist, wird der Wirkungsgrad umso größer, je höher T₁ ist, das heißt, je größer der Temperaturunterschied zwischen dem heißen und dem kälteren Wärmespeicher ist.
Auch für Dampfmaschinen (die ja einen realen Kreisprozess durchlaufen, in dem zusätzliche Verluste beispielsweise durch Reibung auftreten) gilt, dass der Wirkungsgrad umso höher ist, je höher T₁ ist (wobei T₂ gleich bleibt). Erzeugt man im Kessel also höhere Temperaturen (was gleichbedeutend mit einem höheren Druck im Kessel ist), erzielt man einen größeren Wirkungsgrad. Bei einer realen Maschine müssen aber natürlich noch andere Wirkungsgrade berücksichtigt werden – der mechanische, der zum Beispiel Reibungsverluste berücksichtigt; Wirkungsgrade, die die Umwandlung von mechanischer in elektrische Energie erfassen; solche für die Umsetzung von in Brennstoffen enthaltener Energie und so weiter.

Carnotscher Kreisprozess

Michaela, die Assistentin für alles Philosophische und Psychologische, Yoga und Wellness. Chronisch unfrisiert liebt sie alles Chaotische, Kreative und möchte deshalb natürlich Leben im Universum haben.
Luzie, die Assistentin aus dem Untergeschoss, zuständig für alles Brennbare und Explosive, ist der Untergang aller Ordnung und Symmetrie und der Ruin der Nerven ihrer Kolleginnen.
Laplacie, der Laplacesche Dämon, der als fleißiger HiWi immer für Ordnung sorgt und für den nur die Quantenmechanik schlimmer ist als das Aufeinandertreffen aller drei Kolleginnen.
Gott, der Chef, der mit unerschütterlicher Ruhe die Kolleginnen und ihre Arbeiten dahin lenkt, wo er sie hinhaben will, zu einer funktionierenden Physik und irgendwann der Entstehung von Bakterien, Quallen, Nashörnern und anderen Lebewesen.
Gabriela, die Assistentin für Naturwissenschaften. Stets exakt frisiert hält sie hochsymmetrische Zustände für den Inbegriff von Schönheit und steht der Idee, Leben und das damit verbundene Chaos im Universum entstehen zu lassen, mit Skepsis, um nicht zu sagen, tief empfundenem Abscheu gegenüber.

Gabriela entwickelte eine Idee. „Ein idealer Kreisprozess. Das ist es, was wir brauchen. Um die Verluste so klein wie möglich zu halten. Oder eigentlich völlig zu beseitigen. Sonst wäre es ja kein idealer Kreisprozess.“
Sie schickte den Dämon los, ein Material zu suchen, das unendlich gut Wärme leitete, und eins, das Wärme überhaupt nicht leitete. Aus dem ideal Wärme leitenden Material musste er dann zwei Wärmespeicher bauen, aus dem ideal wärmeisolierenden Material ein Gefäß mit einem Kolben. Nur der Boden des Gefäßes musste aus dem Wärme leitenden Material bestehen.
Sie füllte nun ein ideales Gas in das Gefäß mit dem Kolben, füllte den einen Wärmespeicher mit viel Wärme, den anderen mit weniger Wärme und brachte das Gas auf die höhere Temperatur des heißeren Wärmespeichers. Dann setzte sie den Gasbehälter mit der Wärme leitenden Fläche auf den heißen Wärmespeicher und wartete. Vorher sorgte sie aber noch dafür, dass der Außendruck stets verschwindend wenig kleiner war als der Druck im Gasgefäß. „Verschwindend wenig“ bedeutete, dass der Druckunterschied kleiner war als jeder noch so kleine Wert – wie klein auch immer man sich so einen Druckunterschied denken kann, Gabrielas Druckunterschied war noch kleiner. Aber natürlich nicht Null. Denn es musste ja ein Druckunterschied da sein. Der Kolben setzte sich aufgrund des Druckunterschiedes in Bewegung – sehr, sehr langsam zwar, aber er bewegte sich, das Gas dehnte sich aus. Eigentlich hätte es sich ja nun wegen der Ausdehnung abkühlen müssen, aber durch die unendlich gut Wärme leitenden Wände von Wärmespeicher und Gefäß drang Wärme ein und glich den Temperaturunterschied in jedem Moment sofort aus. Da der ganze Vorgang so langsam vor sich ging – genau genommen unendlich langsam, weil der Druckunterschied ja verschwindend klein war – war der Temperaturausgleich ohne zeitliche Verzögerung möglich. Das Gas dehnte sich also aus, ohne dabei kälter zu werden. Die innere Energie des Gases blieb also konstant. Dabei verrichtete das Gas die ganze Zeit Arbeit an dem Kolben. Dann musste Laplacie auf Gabrielas Anweisung das Gasgefäß vom Wärmespeicher herunterheben und auf ein wärmeisolierendes Podest setzen. Nun war kein Wärmeaustausch mehr möglich. Aufgrund des Druckunterschiedes bewegte sich der Kolben immer noch, aber jetzt nahm die Temperatur im Gas ab. Die innere Energie des Gases verringerte sich – die vom Gas verrichtete Arbeit ging also nun auf Kosten der inneren Energie das Gases. Genau in dem Moment, in dem das Gas die niedrigere Temperatur des zweiten Wärmespeichers erreicht hatte, hob Laplacie es auf eben diesen Wärmespeicher und änderte die Druckverhältnisse so, dass der Außendruck nun verschwindend größer was als der Druck im Gas. Der Kolben bewegte sich deshalb nun nach innen und komprimierte das Gas, leistete also Arbeit am Gas. Die Erwärmung des Gases blieb aus, weil die ideale Kopplung an den kälteren Wärmespeicher dafür sorgte, dass die Wärme augenblicklich an diesen Speicher abgegeben wurde und so ein sofortiger Temperaturausgleich erreicht wurde. Als nächstes kam das Gasgefäß wieder auf das wärmeisolierende Podest. Während der Kolben sich weiter nach innen bewegte – jetzt also ohne Temperaturausgleich im Gas – stieg die Temperatur im komprimierten Gas. Als die Temperatur des wärmeren Wärmespeichers erreicht war, setzte Laplacie das Gasgefäß wieder auf diesen und der ganze Prozess begann von vorn. Oder er hätte jedenfalls von vorn begonnen, wenn Gabriela das Ganze nicht an dieser Stelle abgebrochen hätte. Schließlich hatte ein Umlauf schon unendlich lange gedauert und sie wollte ja auch mal weiterkommen. Im Prinzip wäre es durchaus möglich, den Kreisprozess bis in alle Ewigkeit durchlaufen zu lassen – da sie unendlich große Wärmespeicher gebaut hatte, änderte sich deren Temperatur durch Wärmezu- oder -abfuhr nicht. Es musste also auch nichts geheizt werden und das Gas hatte nach einem Durchlauf exakt denselben Zustand wie vorher.
Sie maß Wärmemengen und Arbeiten, rechnete eine Weile herum und stellte fest, dass bei dem Durchlauf insgesamt mehr Wärme aus dem wärmeren Speicher aufgenommen als an den kalten abgegeben wurde. Die Differenz hatte das Gas als Arbeit verrichtet. Aber eben auch nur die Differenz – ein Teil der Wärme war an den kalten Wärmespeicher abgegeben und somit nicht in Arbeit umgewandelt worden. Es war also auch mit dieser idealen Maschine nicht möglich, die aufgenommene Wärme vollständig in Arbeit umzuwandeln. Gabriela war zufrieden, der zweite Hauptsatz behielt offenbar seine Gültigkeit …