Dr. Wiebke Salzmann
freie Lektorin und Autorin
Wissenstexte
Physik-Wissen
Corioliskraft
Auf dieser Seite scheinen die Kräfte sehr träge …
www.wissenstexte.de > Physik-Wissen > Mechanik > Coriolis-Kraft
Corioliskraft
Die Coriolis-Kraft ist eine so genannte Trägheitskraft. Um sie zu verstehen, müssen wir uns also zunächst anschauen, was eine Trägheitskraft ist.
Trägheitskräfte
Ein Körper, auf den keine Kräfte wirken, behält aufgrund seiner Massenträgheit den Bewegungszustand bei, den er gerade hat. Befindet sich ein Körper im All, ist er weit ab von jedem Gravitationsfeld oder anderen Kräften. Stößt man diesen Körper mit einer bestimmten Geschwindigkeit in eine bestimmte Richtung an, wird er diese Geschwindigkeit und diese Richtung so lange beibehalten, bis er einen erneuten Stoß erhält (oder eine andere Krafteinwirkung spürt). Das ist nichts anderes als der Impulserhaltungssatz – ohne Krafteinwirkung von außen bleibt der Impuls eines Körpers erhalten. Die Massenträgheit ist also eine „Ausdrucksform“ des Impulserhaltungssatzes.
Das lässt sich auf der Erde nicht ausprobieren, da hier zum einen überall die Gravitation wirkt, zum anderen durch die allgegenwärtige Luft auch ein Reibungswiderstand existiert. Körper, auf die keine Kräfte wirken, gibt es hier also gar nicht. Trotzdem kann man die Massenträgheit täglich spüren – beim Bremsen im Auto oder in der Straßenbahn: Dann spürt man einen Ruck nach vorn, weil der eigene Körper den Vorwärtsimpuls, den er aufgrund der Fahrzeugbewegung hatte, nicht „freiwillig“ aufgibt. Erst wenn eine Kraft auf ihn wirkt – meist in Form von Muskelspannung, im schlimmsten Fall durch einen Mitpassagier oder eine Wand – stoppt er die Vorwärtsbewegung und ändert seinen Impuls entsprechend.
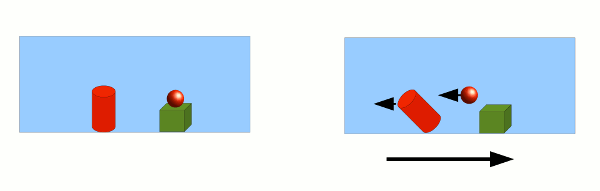
In Abbildung 1 ist der Fall dargestellt, dass ein ursprünglich ruhendes „Fahrzeug“ sich in Bewegung setzt: In dem großen Kasten (dem Fahrzeug) in Abbildung 1 (links) befinden sich ein Zylinder und eine Kugel. Ersterer steht auf dem Boden, letztere liegt auf einem Podest, das mit dem Kasten fest verbunden ist. Setzt sich der Kasten nun in Bewegung (rechts), möchten Zylinder und Kugel ihren alten Bewegungszustand (also den Zustand „keine Bewegung“) erhalten. Der Kugel gelingt das mehr oder weniger – zumindest im schwerelosen Raum bleibt sie an ihrem alten Ort schweben, bis die rückwärtige Wand des Kastens auf sie trifft, sie vor sich herschiebt und ihr so die Kastenbewegung aufzwingt. Auf der Erde lässt die Gravitation die Kugel nach unten fallen. Der Zylinder wird durch die Reibung zwischen ihm und dem Kastenboden gehindert, seine alte Position beizubehalten. Der untere Teil wird aufgrund der Reibung mit dem fahrenden Kasten mitgezogen, der obere möchte bleiben, wo er ist, und in der Folge kippt der Zylinder um.
- Abb. 1 ¦ Trägheitskräfte

- Die Gegenstände im Kasten spüren eine Trägheitskraft, sobald dieser sich in Bewegung setzt.
So stellt sich der Ablauf für einen neben dem Kasten stehenden Beobachter dar. Versetzen wir uns nun in den Kasten hinein, an die Stelle des Zylinders, als seien wir bspw. ein stehender Passagier. Beim Anfahren einer Straßenbahn spürt der Passagier eine Kraft, die ihn nach hinten fallen lässt. (Entsprechend spürt man beim Abbremsen der Straßenbahn eine Kraft, die einen nach vorn fallen lässt.) Aus der Sicht des Passagiers fliegt die Kugel nach hinten – denn er bezieht alle Bewegungen auf das Innere des Kastens, dieser stellt für ihn das (ruhende) Bezugssystem dar.
In der Beschreibung der Situation von außen gab es jedoch keine Kraft, die den Passagier/den Zylinder nach hinten gestoßen hätte. Es ist nichts und niemand zu sehen, das oder der die Kraft hätte ausüben können. Der außen stehende Beobachter sieht nur einen Körper, der seinen ursprünglichen Bewegungszustand beibehalten will – der sich aufgrund seiner Massenträgheit einer Änderung seines Bewegungszustandes widersetzt. Von außen betrachtet, fällt nicht der obere Teil des Zylinders nach hinten, sondern der untere Teil wird mit dem anfahrenden Fahrzeug mitgezerrt (aufgrund der Reibung), bzw. die Kugel bewegt sich gar nicht. Denn der außen stehende Beobachter bezieht alles, was er sieht, auf den Außenraum, dieser ist für ihn das ruhende Bezugssystem.
Bei der Kraft, die den Zylinder umkippen lässt, handelt sich also um eine Kraft, die zwar der Passagier (oder der Zylinder) spürt, die aber für einen Beobachter von außen nicht vorhanden ist. Der Unterschied zwischen dem außen stehenden Beobachter und dem Passagier im Fahrzeug ist, dass der Passagier sich in einem beschleunigten Bezugssystem befindet (dem Fahrzeug nämlich), während der Beobachter in einem nicht beschleunigten Bezugssystem steht (dem Straßenrand zum Beispiel). Dabei ist es nicht wichtig, ob der Straßenrand wirklich ruht im Sinne von still steht – entscheidend ist, dass er sich nicht beschleunigt bewegt. Die Kraft existiert also nur im beschleunigten Bezugssystem – deshalb nennt man sie auch Scheinkraft.
Für den äußeren Beobachter hält die Trägheit der Kugel sie in Ruhe, da keine Kraft auf sie wirkt; der innere Beobachter nimmt jedoch wahr, dass die Kugel sich mit dem Anfahren des Kastens plötzlich nach hinten in Bewegung setzt. Eine plötzlich einsetzende Bewegung muss jedoch eine Kraft als Ursache haben, deshalb wirkt aus seiner Sicht eine Trägheitskraft. Da sie daher eine Folge der Trägheit eines Körpers gegenüber Veränderungen seines Bewegungszustandes ist, heißt sie eben auch Trägheitskraft. Diese Bezeichnung ist m. E. die bessere, weil sie direkt auf die Ursache der Kräfte Bezug nimmt. Zudem täuscht der Begriff Scheinkraft leicht darüber hinweg, dass Trägheitskräfte durchaus Auswirkungen haben können, wenn bspw. der Passagier in der Bahn wirklich umfällt.
Trägheitskräfte existieren also nur in beschleunigten Bezugssystemen; für einen Beobachter von außen existieren sie nicht – für ihn gibt es nur die (Massen-)Trägheit selbst.
Noch einmal anders formuliert: Der außen stehende Beobachter sieht ein Objekt, das seinen Bewegungszustand erhält (dem Impulserhaltungssatz genügt). Der innen stehende Beobachter nimmt seine eigene beschleunigte Bewegung nicht wahr, für ihn ändert daher das Objekt seinen Bewegungszustand bzw. sein Impuls ändert sich aus seiner Perspektive – das geht aber nicht ohne Kraft. Daher nimmt der innere Beobachter eine Trägheitskraft wahr.
Aber natürlich stellen sich für beide Beobachter, den außen wie den innen stehenden, die jeweiligen Bewegungen gleich dar. Die Kugel im blauen Kasten bspw. prallt für beide irgendwann gegen die Rückwand des Kastens – nur nimmt der äußere Beobachter die Kugel als ruhend und den Kasten als nach vorn fahrend wahr, der innere dagegen nimmt die Kugel als nach hinten fliegend wahr, weil er selbst sich mit dem Kasten nach vorn bewegt, dieser sich also relativ zum inneren Beobachter in Ruhe befindet.
Die Coriolis-Kraft
Sich drehende Bezugssysteme sind immer beschleunigte Bezugssysteme, da Körper auf Kreisbahnen ständig ihre Richtung ändern. (Beschleunigungen können nicht nur Änderungen im Betrag der Geschwindigkeit verursachen, sondern auch in ihrer Richtung.) Ein Körper, der in einem sich drehenden Bezugssystem ruht, spürt die Zentrifugalkraft. Bewegt sich der Körper in einem sich drehenden Bezugssystem, spürt er nicht nur die Zentrifugalkraft, sondern zusätzlich auch noch die Corioliskraft. Anschaulich kommt diese daher, dass sich das drehende Bezugssystem unter dem Körper weiterbewegt. Deshalb sieht es für einen Beobachter im rotierenden Bezugssystem aus, als wirke auf den Körper eine Kraft, die diesen aus seiner Bahn ablenkt.
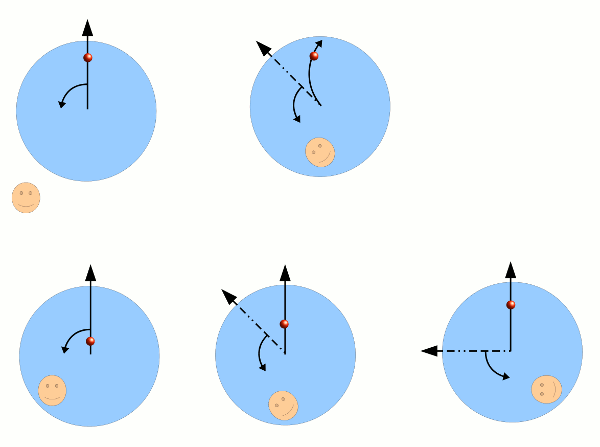
Als Beispiel stellen wir uns gedanklich auf eine sich drehende Scheibe. Nun fliegt ein Gegenstand vom Mittelpunkt der Scheibe aus radial nach außen (Abbildung 2, oben links). Für einen neben der Scheibe stehenden Beobachter sieht das auch genau so aus – der Gegenstand fliegt radial nach außen. Für uns auf der sich drehenden Scheibe jedoch, die wir uns entsprechend mitdrehen, wird der geradlinige, radiale Flug zu einem gekrümmten (Abbildung 2, oben rechts). Das kommt zustande, weil wir uns mit der Drehung der Scheibe von der Bahn des Körpers entfernen (Abbildung 2, unten). Der durchgezogene Pfeil symbolisiert die geradlinige Bahn des Körpers, wie sie ein äußerer Beobachter sieht; der gestrichelte Pfeil die geradlinige Bahn, wo sie wäre, wenn sie sich ebenfalls mit der Scheibe drehen würde, was sie natürlich nicht tut. Da der sich drehende Beobachter sich selbst aber in Ruhe wähnt, bezieht er alle Bewegungen auf sich. Ein sich geradlinig bewegender Körper müsste also für diesen mitbewegten Beobachter dem gestrichelten Pfeil folgen (der gestrichelte Pfeil dreht sich mit). Da der Körper sich aber immer weiter von diesem Pfeil entfernt (bzw. der Pfeil entfernt sich vom Körper), wirkt die Bahn des Körpers auf den mitbewegten Beobachter gekrümmt. Da sich eine Bahn eines Körpers niemals von allein krümmt – das widerspräche dem Trägheitsgesetz, also dem Impulserhaltungssatz – muss also aus der Sicht des sich drehenden Beobachters eine Kraft auf den Körper wirken – die Corioliskraft.
- Abb. 2 ¦ Corioliskraft
-
Oben: Der außen stehende Beobachter sieht den Gegenstand geradlinig und kräftefrei fliegen (Gravitation und Luftreibung vernachlässigen wir) (links); der Beobachter auf der sich drehenden Scheibe sieht eine Corioliskraft wirken, die die Bahn des Gegenstandes krümmt (rechts).
Unten: Der gestrichelte Pfeil stellt die radiale Richtung aus der Sicht des sich mitdrehenden Beobachters dar – auch der Pfeil muss sich daher mitdrehen. Von dieser sich drehenden radialen Richtung weicht die tatsächlich radiale Flugbahn ab.
Coriolis-Kraft auf der Erde
Die Coriolis-Kraft wirkt nicht nur bei radial gerichteten Bewegungen, sondern bei allen Bewegungen in rotierenden Bezugssystemen – mit der Einschränkung, dass sie nur auf die Bewegungskomponenten wirkt, die senkrecht zur Drehachse gerichtet sind. Ist die Bewegung parallel zur Drehachse gerichtet, ist die Corioliskraft Null.
Auch die Erde ist ein sich drehendes Bezugssystem und bei großräumigen Bewegungen wie Winden macht sich die Corioliskraft bemerkbar – wie man an den großen Tiefdruckwirbeln sieht. Die Corioliskräfte auf der Erde sind relativ klein und können daher meist vernachlässigt werden. Bemerkbar machen sie sich erst bei großräumigen Bewegungen wie Luftströmungen zwischen Tief- und Hochdruckgebieten. Hier strömt die Luft nicht direkt vom Hochdruckgebiet zum Tiefdruckgebiet, sondern wird von der Corioliskraft auf Kreisbahnen um die Hochs bzw. Tiefs herum gezwungen – man kennt die Wolkenwirbel aus Satellitenaufnahmen. Auf der Nordhalbkugel drehen sich die Luftströmungen gegen den, auf der Südhalbkugel im Uhrzeigersinn. Entsprechend gilt dies natürlich auch für tropische Wirbelstürme.
Die Richtung der Corioliskraft ist immer senkrecht zur Drehachse und senkrecht zur Relativbewegung des Körpers, auf den sie wirkt.
Sehen wir uns zunächst eine Bewegung am Äquator an. Ein Luftteilchen soll sich erst einmal am Äquator genau von Süd nach Nord bewegen. Damit ist seine Bewegung parallel zur Drehachse (der Erdachse) gerichtet und es wirkt keine Corioliskraft.
Nun soll sich das Luftteilchen etwas nördlich vom Äquator von Süd nach Nord bewegen. Wir müssen uns erst darüber klar werden, was „von Süd nach Nord“ bedeutet: Auf der Erde bedeutet dies, das Teilchen bewegt sich entlang eines Längenkreises.
Dabei sind zwei Dinge zu beachten:
Zum einen nimmt wegen der Kugelform der Erde der Radius der Breitenkreise in Richtung Pol ab. Da die Erde sich mit einheitlicher Winkelgeschwindigkeit um sich selbst dreht, bedeutet dies, dass die Bahngeschwindigkeit der Drehung am Äquator ihr Maximum hat und in Richtung Pol abnimmt. (Gemeint ist die Bahngeschwindigkeit eines Punktes auf der Erdoberfläche.)
Zum andern bewegt sich das Luftteilchen ebenfalls mit der Erddrehung mit.
Das bedeutet, bevor das Luftteilchen anfängt mit seiner Nord-Süd-Bewegung, dreht es sich mit der Erde mit (wie die gesamte Atmosphäre), d. h. von West nach Ost. Für einen außen stehenden Beobachter bewegt es sich also auf einer Kreisbahn um die Erdachse; für einen Beobachter auf der Erdoberfläche steht es still.
Nun setzt die Süd-Nord-Bewegung ein. Dabei behält es die Drehbewegung längs des Breitenkreises nach Osten bei. Dies ist eine Folge der Drehimpulserhaltung – der Drehimpuls bleibt wie der Impuls erhalten, so lange keine Kräfte einwirken. Für den äußeren Beobachter hat die Bewegung des Teilchens also zwei Komponenten: nach wie vor die Drehbewegung nach Osten und zusätzlich die Bewegung nach Norden. Wenn dieses Teilchen nun in höhere Breiten gerät, gerät es damit in Bereiche, deren Bahngeschwindigkeit nach Osten geringer ist als seine eigene. Während am Äquator das Teilchen sich relativ zur Erdoberfläche nicht nach Osten bewegt hat, weil Erdoberfläche und Atmosphäre sich gleich schnell nach Osten drehen, bewegt das Teilchen sich nun schneller nach Osten als der darunterliegende Bereich der Erdoberfläche – seine ursprünglich in Süd-Nord gerichtete Bewegung erhält nun (relativ zur Erdoberfläche unter ihm) eine Komponente nach Osten. Damit kippt die Bewegung aus der Süd-Nord-Richtung nach rechts in eine Südwest-Nordost-Richtung und schließlich in West-Ost-Richtung. (Entsprechend wird ein Teilchen, das sich in Nord-Süd-Richtung bewegte, in eine Ost-West-Bewegung gebracht.)
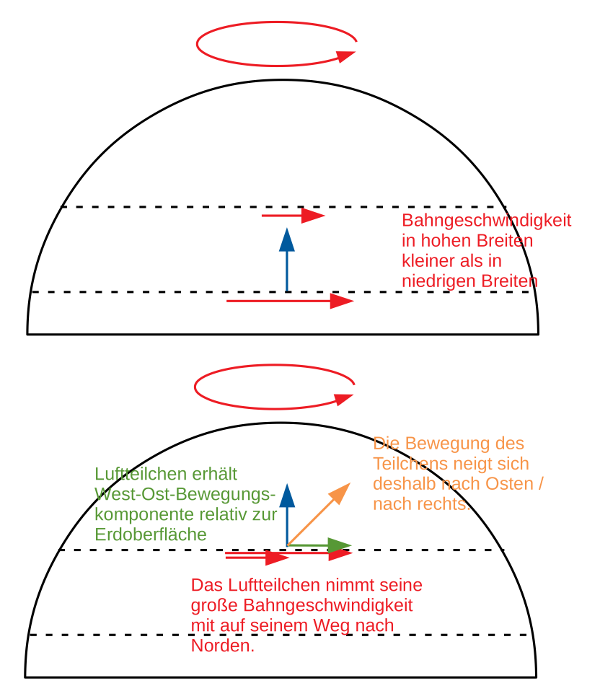
- Abb. 3 ¦ Einfluss der Erddrehung
-
Dargestellt ist die Nordhalbkugel der Erde.
Oben: Auf einem niedrigen Breitenkreis ist die Bahngeschwindigkeit der Erddrehung kleiner als auf einem Kreis hoher Breite (rote Pfeile). Ein Luftteilchen soll sich in Richtung Norden in Bewegung setzen (blauer Pfeil) – die Nord-Bewegung findet relativ zur Erdoberfläche statt, d. h., das Teilchen macht die Drehung mit. Es hat relativ zur Erdoberfläche also keine Geschwindigkeitskomponente in West-Ost-Richtung.
Unten: Das Teilchen ist auf einem Breitenkreis höherer Breite angekommen. Aufgrund der Drehimpulserhaltung hat es seine ursprüngliche Bahngeschwindigkeit beibehalten, ist nun also bezogen auf die Bahngeschwindigkeit dieses Breitengrades zu schnell in Richtung Osten unterwegs. Seine Bewegung hat jetzt eine Komponente in Ost-Richtung, die der Differenz der Bahngeschwindigkeiten der beiden Breitengrade entspricht (grüner Pfeil). Damit ist seine Bewegung (relativ zur Erdoberfläche) nun eine Kombination aus seiner Süd-Nord-Bewegung (blau) und dieser West-Ost-Bewegung (grün). Im Ergebnis bewegt es sich nun von Südwest nach Nordost (orangefarbener Pfeil).
Bei weiterer Bewegung Richtung Norden wird die Bewegung weiter nach rechts gedreht, bis das Teilchen nach Osten fliegt.
(Der Effekt der zunehmenden Geschwindigkeit aufgrund des abnehmenden Bahnradius ist hier nicht berücksichtigt.)
Dieses Kippen der Bewegungsrichtung einer Nord-Süd-Bewegung nach rechts hat also nur darin seine Ursache, dass die Bahngeschwindigkeit der Erddrehung am Startpunkt der Teilchenbewegung eine andere ist als an ihrem Ende und dass das Teilchen die anfängliche Bahngeschwindigkeit mitnimmt. Auch dies Beibehalten der ursprünglichen Drehbewegung ist wieder die Folge der Trägheit des Teilchens bzw. der Drehimpulserhaltung. Das Teilchen behält seine Bewegung bei, weil es keine äußeren Kräfte gibt, die den Drehimpuls geändert bzw. die Bewegung nach Osten beeinflusst haben.
Ein Beobachter auf der Erdoberfläche nimmt dieses Drehen der Bewegungsrichtung natürlich auch wahr. Er, der sich ebenfalls mit der Erde mitdreht, nimmt die Erddrehung aber nicht als solche wahr. Er empfindet sich selbst als ruhend und betrachtet die Bewegung des Teilchens relativ zu seinem (für ihn ruhenden) Bezugssystem. Relativ zu diesem wird das Teilchen in höheren Breiten aber nach Osten beschleunigt. Eine Beschleunigung bedeutet die Wirkung einer Kraft – der Beobachter auf der Erdoberfläche nimmt daher eine Trägheitskraft wahr, die Corioliskraft.
Und der Einfachheit halber reden wir daher auch dann von der Corioliskraft, wenn wir bspw. tropische Wirbelstürme auf Satellitenbildern sehen, sie also eigentlich von außen betrachten. (Dasselbe tun wir ja auch, wenn wir von außen ein Kettenkarussell beobachten – auch da sprechen wir von der Zentrifugalkraft, obwohl diese nur einen Insassen spürbar ist. Von außen betrachtet sollten wir auch hier von der Trägheit sprechen. Aber wir wissen alle aus Erfahrung, wie es sich anfühlt, an die Seitenlehne gepresst zu werden und aufgrund dieser Erfahrung nehmen wir die Innenperspektive häufig auch dann an, wenn wir eigentlich von außen schauen.)
Der Effekt wird noch verstärkt, weil wegen der Drehimpulserhaltung die Bahngeschwindigkeit abhängig ist vom Abstand zur Drehachse: Je näher ein Objekt der Drehachse kommt, desto schneller wird es. (Deshalb ziehen Eiskunstläufer die Arme ein, wenn sie ihre Drehung beschleunigen wollen.)
Denn da der Drehimpuls proportional zur Bahngeschwindigkeit und zum Abstand der Drehachse ist, muss die Geschwindigkeit zunehmen, wenn der Abstand abnimmt. Nur dann bleibt der Drehimpuls erhalten.
Die Radien der Breitenkreise werden mit zunehmender geografischer Breite aber immer kleiner. Das Teilchen nähert sich dabei also immer mehr der Erdachse und bewegt sich daher mit zunehmender Annäherung an den Pol auch aus diesem Grund noch schneller nach Osten, wodurch seine Bewegung noch stärker nach rechts gedreht wird.
(Bei einer Bewegung Richtung Äquator nimmt die Geschwindigkeit entsprechend ab, da in dieser Richtung der Radius der Breitenkreise zunimmt.)
Zu beachten ist noch, dass nur auf der Nordhalbkugel die Teilchenbewegung nach rechts gedreht wird, auf der Südhalbkugel kommt es zu einer Linksdrehung.
Wie kommt es nun aber zu Wirbelstürmen? Um einen Wirbel zu erhalten, brauchen wir auch noch die Rechtsdrehung der Ost-West-Bewegung. Diese kommt streng genommen nicht durch eine Corioliskraft, sondern durch die Zentrifugalkraft zustande. Da dies aber ebenfalls eine Trägheitskraft ist, spricht man der Einfachheit halber im Fall der Tropischen Wirbelstürme hier ebenfalls von Corioliskraft und kommt so zu der allgemeinen Aussage: Durch die Corioliskraft werden Bewegungen auf der Nordhalbkugel nach rechts und auf der Südhalbkugel nach links abgelenkt.
Zurück zu der Frage, was bei einer Bewegung in Ost-West-Richtung die Ablenkung bewirkt. Bei einer Ost-West-Bewegung bewegt sich das Teilchen entlang eines Breitenkreises. Beginnen wir wieder mit dem Fall, dass das Teilchen relativ zu seiner Umgebung und relativ zur Erdoberfläche still steht. Dann hat es genau die zum jeweiligen Breitenkreis gehörende Bahngeschwindigkeit. Auf das Teilchen wirkt die Gravitation der Erde, die es anzieht und auf der Kreisbahn hält. Denn ohne die Erdanziehung würde es aufgrund seiner Massenträgheit tangential und geradlinig davonfliegen. Diese Massenträgheit muss in jedem Moment von der Gravitation „bekämpft“ werden, das Teilchen gegen seine Trägheit auf der Bahn gehalten werden. Diesen Trägheitswiderstand nimmt man als Zentrifugalkraft wahr, wenn man bspw. einen Gegenstand an einem Seil um sich herumschleudert. Das Verhältnis von Gravitation und Zentrifugalkraft bewirkt eine bestimmte Kreisbahn um die Erde, auf der das Teilchen nun fliegt.
Da die Erdanziehung zum Erdmittelpunkt gerichtet ist, die Zentrifugalkraft aber senkrecht zur Erdachse nach außen, stehen beide in einem Winkel zueinander. Die Erdkugel selbst hat sich unter dem Einfluss dieser Kräfte verformt und zwar so, dass die Gewichtskraft (die dem Summenvektor aus Gravitation und Zentrifugalkraft entspricht) überall senkrecht zur Erdoberfläche steht.
Das Teilchen befindet sich also auf seiner Kreisbahn. Nun sollen irgendwelche Druckgebiete in der Atmosphäre bewirken, dass das Teilchen zusätzlich nach Osten beschleunigt wird. Damit ist die Zentrifugalkraft größer geworden. Da die Gravitation aber natürlich unverändert bleibt, zeigt der Summenvektor beider Kräfte nicht mehr senkrecht zur Erdoberfläche. Es gibt nun eine zusätzliche Komponente, die das Teilchen südwärts ablenkt. (Entsprechend wird es bei einer Bewegung nach Westen nach Norden abgelenkt.)
Auch hier haben wir also eine Rechtsablenkung der Bewegung (auf der Südhalbkugel entsprechend nach links).
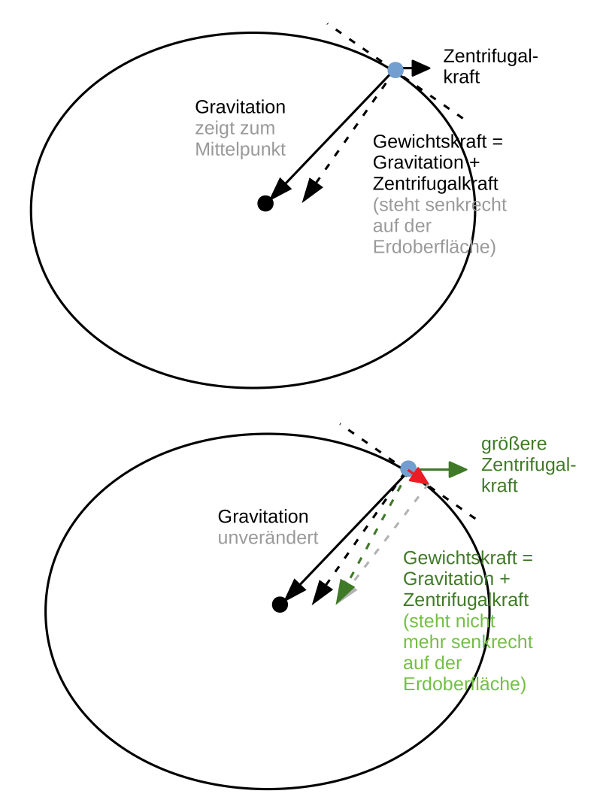
- Abb. 4 ¦ Zentrifugalkraft als „Corioliskraft“
-
Die gestrichelte Linie an der Erdoberfläche stellt die Tangente an den fraglichen Punkt (blau) dar.
Oben: Die Erdkugel hat sich unter dem Einfluss der Drehung und der dabei auftretenden Zentrifugalkraft verformt – sie ist keine Kugel, sondern ein Ellipsoid. Diese Verformung führt dazu, dass Gewichtskraft und Gravitation nicht mehr exakt dasselbe sind (obwohl man im Allgemeinen beide problemlos gleichsetzen kann). Die Gravitation zeigt immer noch zum Erdmittelpunkt, steht aber nicht mehr senkrecht auf der Erdoberfläche, wie es bei einer Kugel der Fall wäre. Die Gewichtskraft hingegen, die sich als Vektorsumme aus Gravitationskraft und Zentrifugalkraft ergibt, steht senkrecht auf der Erdoberfläche, zeigt aber nicht exakt zum Erdmittelpunkt. Die Gewichtskraft zieht uns also senkrecht nach unten.
Unten: Hat ein Teilchen nun in Ost-Richtung eine höhere Geschwindigkeit als der Erddrehung entspräche, erhöht sich die Zentrifugalkraft, die es spürt (grüner Pfeil). Damit wird der Summenvektor aus Gravitation und Zentrifugalkraft verdreht (grüner, gestrichelter Pfeil). Dieser neue Summenvektor steht nicht mehr senkrecht auf der Erdoberfläche, sondern hat eine Komponente parallel zu dieser (roter Pfeil). Diese Parallelkomponente ist gleichbedeutend mit einer Kraft, die das Teilchen nun nach Süden ablenkt.
Foucaultsches Pendel
Man kann die Corioliskraft nutzen, um die Erddrehung nachzuweisen, und zwar mithilfe des Foucaultschen Pendels. Sie bewirkt nämlich, dass sich die Schwingungsebene eines Pendels während des Pendelns (scheinbar) ändert: die Schwingungsebene scheint sich zu drehen.
Wie schnell sich ein Pendel dreht, hängt deshalb davon ab, wo man es aufhängt – das heißt, auf welcher geografischen Breite. Da die Corioliskraft nur auf Bewegungen wirkt, die eine Komponente senkrecht zur Erdachse haben, ist ihr Einfluss abhängig von der geografischen Breite. An den Polen ist jede horizontale Bewegung senkrecht zur Drehachse gerichtet, hier ist der Effekt also maximal. Die Erde dreht sich genau unter dem Pendel weg – was für einen Beobachter neben dem Pendel so aussieht, als drehe sich die Schwingungsebene des Pendels. Der Beobachter ist ja fest mit der Erde verbunden, dreht sich also mit ihr mit, während das Pendel frei hängt, sich also nicht mitdreht. Da der Beobachter von seiner eigenen Drehung nichts merkt, glaubt er das Pendel sich drehen zu sehen. Nach 24 Stunden hat das Pendel wieder seine alte Schwingungsebene erreicht. Am Äquator verschwindet die Drehung der Schwingungsebene ganz, da sich hier der Abstand des Pendels zur Drehachse der Erde nicht ändert, wenn es in Nord-Süd-Richtung ausgelenkt wird. Wird es in Ost-West-Richtung ausgelenkt, wirkt die Corioliskraft nach oben bzw. unten, was keine Drehung der Schwingungsebene zur Folge hat. Bei einer Auslenkung in einem anderen Winkel, überlagern sich beide Effekte – was aber auch keine Drehung bewirkt, da keiner der Einzeleffekte dies tut. In Breiten zwischen Pol und Äquator liegt auch die Wirkung der Corioliskraft zwischen beiden Extremen, die Änderung der Schwingungsebene ist entsprechend kleiner als an den Polen. Das heißt, das Pendel braucht länger als einen Tag, um seine ursprüngliche Schwingungsebene wieder zu erreichen.
- Abb. 6 ¦ Foucaultsches Pendel
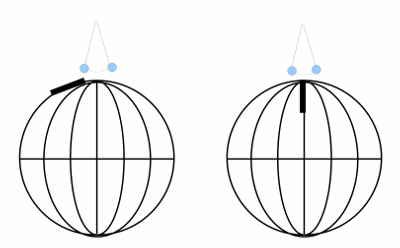
- Ein in Polnähe auf gehängtes Pendel soll zunächst parallel zum dick markierten Längenkreis schwingen (links). Die Schwingungsebene des Pendels ändert sich nicht, wohl aber die Lage des Längenkreises, während die Erde sich dreht. Nach einer Vierteldrehung ist der gekennzeichnete Längenkreis senkrecht zur Schwingungsebene des Pendels gerichtet (rechts).
© Wiebke Salzmann, Juli 2009
