Dr. Wiebke Salzmann
freie Lektorin und Autorin
Wissenstexte
Physik-Wissen
elastische Stöße
Auf dieser Seite wimmelt es ausnahmsweise mal von Formeln …
www.wissenstexte.de > Physik-Wissen > Mechanik > Elastische Stöße
Elastischer Stoß zweier Kugeln
– Stoß zweier Kugeln
– gleich schwere Kugeln
– eine Kugel ruht
– Newtonsches Kugelpendel
Wir beschränken uns hier auf Kugeln, die sich beim Zusammenstoß nicht dauerhaft verformen – wie beispielsweise Knetgummikugeln dies tun würden. Dann nämlich handelt es sich um einen elastischen Stoß. Außerdem sollen die Kugeln gerade aufeinanderprallen, das heißt, die Bahnen, auf denen sie aufeinander zu fliegen oder rollen, liegen auf einer Linie.
Erhaltungssätze für Energie und Impuls
Wenn die Kugeln sich beim Stoß nicht verformen, wird auch keine Energie in Wärme oder Verformungsenergie umgewandelt. Die einzige Energieform, die wir hier betrachten müssen, ist also die kinetische Energie. Der Energieerhaltungssatz bedeutet daher in diesem Fall, dass die kinetische Energie der Kugeln vor und nach dem Stoß dieselbe sein muss – wohlgemerkt, die Gesamtbewegungsenergie muss erhalten bleiben, also die Summe der Energien der beiden Kugeln; die Energie der einzelnen Kugeln kann sich sehr wohl ändern.
Die kinetische Energie ist: Ekin = 1/2 ⋅ m v2, wobei m die Masse des betrachteten Körpers ist (also in unserem Fall die Masse der Kugel) und v die Geschwindigkeit.
Bezeichnen wir die Größen, die zur ersten Kugel gehören, mit dem Index 1 und diejenigen, die
zur zweiten Kugel gehören, mit dem Index 2, ist also
die kinetische Energie für die erste Kugel:
Ekin,1 = 1/2 ⋅ m1 v12;
und die kinetische Energie für die zweite Kugel:
Ekin,2 = 1/2 ⋅ m2 v22.
Die Gesamtenergie der beiden Kugeln ist die Summe der beiden einzelnen Energien:
Ekin,gesamt = Ekin,1 + Ekin,2 = 1/2 ⋅ m1 v12 + 1/2 ⋅ m2 v22.
Außer dem Energieerhaltungssatz muss auch der Impulserhaltungssatz gelten, das heißt, der
Gesamtimpuls beider Kugeln muss vor und nach dem Stoß derselbe sein – die Summe der Impulse
beider Kugeln darf sich also nicht ändern, wohl aber die Impulse der einzelnen Kugeln. Der Impuls
p eines Körpers setzt sich zusammen aus Masse m und Geschwindigkeit v:
p = m v.
Der Impuls der ersten Kugel ist also p1 = m1 v1,
der Impuls der zweiten Kugel ist p2 = m2 v2.
Der Gesamtimpuls der beiden Kugeln ist wiederum die Summe der Impulse der einzelnen Kugeln:
pges = p1 + p2 = m1 v1 + m2 v2.
(Dass man die beiden Impulse so einfach addieren kann, liegt daran, dass wir vorausgesetzt hatten, dass die Bahnen beider Kugeln auf einer Linie liegen sollen. Würden die Bahnen einen Winkel bilden, könnte man die Impulse nicht so einfach addieren, da Impulse Vektoren sind. Man muss also außer ihrem Betrag immer auch ihre Richtung berücksichtigen und die Regeln der Vektoraddition anwenden. In unserem Spezialfall vereinfacht sich die Addition jedoch zu einer gewöhnlichen Addition.)
Der Stoß
Bei dem Stoß der beiden Kugeln können wir davon ausgehen, dass die Massen der Kugeln sich nicht verändern. Die Geschwindigkeiten dagegen werden sich verändern. Wir müssen also unterschiedliche Bezeichnungen für die Geschwindigkeiten der Kugeln vor und nach dem Stoß benutzen: Für die Geschwindigkeit vor dem Stoß nehmen wir das gewohnte v, für diejenige nach dem Stoß nehmen wir u.
Ist die kinetische Energie der beiden Kugeln vor dem Stoß:
Ekin,gesamt,vor = Ekin,1 + Ekin,2 = 1/2 ⋅ m1 v12 + 1/2 ⋅ m2 v22
so ist sie nach dem Stoß:
Ekin,gesamt,nach = Ekin,1 + Ekin,2 = 1/2 ⋅ m1 u12 + 1/2 ⋅ m2 u22
Wegen des Energieerhaltungssatzes müssen die Energien vor und nach dem Stoß gleich sein:
Ekin,gesamt,vor = Ekin,gesamt,nach
und damit gilt also:
(1) Ekin,1 + Ekin,2 = 1/2 ⋅ m1 v12 + 1/2 ⋅ m2 v22 = 1/2 ⋅ m1 u12 + 1/2 ⋅ m2 u22
Den Faktor 1/2 kann man noch herauskürzen:
m1 v12 + m2 v22 = m1 u12 + m2 u22
Entsprechendes gilt auch für die Impulse. Der Impuls vor dem Stoß ist:
pges = m1 v1 + m2 v2;
der Impuls nach dem Stoß ist:
pges = m1 u1 + m2 u2.
Da auch der Impulserhaltungssatz gelten muss, gilt:
pges,vor = pges,nach
und damit:
(2) m1 v1 + m2 v2 = m1 u1 + m2 u2.
Wir haben mit den Erhaltungssätzen nun also zwei Gleichungen 1 und 2, mit denen wir die
Geschwindigkeiten der Kugeln nach dem Stoß bestimmen können, also die beiden Unbekannten u1
und u2 berechnen können. Es ergeben sich folgende Formeln:
(3) 
Spezialfälle
Für einen konkreten Stoß muss man also nun die Werte für die Massen m1 und m2 der Kugeln und ihre Anfangsgeschwindigkeiten v1 und v2 in die Gleichungen einsetzen und diese nach den Endgeschwindigkeiten u1 und u2 auflösen.
Einige Spezialfälle lassen sich auch untersuchen, ohne Werte für einen bestimmten Stoß einsetzen zu müssen. Diese werden wir und im Folgenden ansehen. In den Grafiken ist die grüne Kugel immer Kugel 1 mit Masse m1, die rote ist Kugel 2 mit Masse m2.
1. Beide Kugeln sind gleich schwer, es gilt also m1 = m2.
Die Differenzen m1 − m2 und m2 − m1
werden also null, und wir können auch für m2 die Masse m1 einsetzen (oder umgekehrt, das spielt
keine Rolle).
Damit wird aus den Gleichungen 3 für die Endgeschwindigkeiten u1 und u2:
(4) 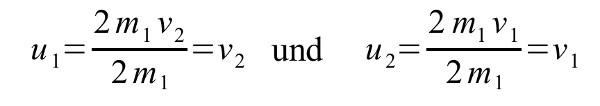
Das bedeutet, die Endgeschwindigkeit der ersten Kugel ist gleich der Anfangsgeschwindigkeit der
zweiten Kugel und umgekehrt. Die Kugeln tauschen ihre Geschwindigkeiten also einfach aus.
Die zweite Kugel fliegt auf die erste zu, kehrt nach dem Stoß ihre Bewegungsrichtung um, wodurch
sie sich in die Richtung bewegt, in der die erste Kugel vor dem Stoß unterwegs war. Außerdem hat
die Geschwindigkeit der zweiten Kugel nach dem Stoß auch den Betrag der Geschwindigkeit der
ersten Kugel von vor dem Stoß. Die zweite Kugel setzt also gewissermaßen den Weg der ersten
Kugel mit deren Geschwindigkeit fort, und umgekehrt.
- Abb. 1 ¦ Kugeln gleicher Masse
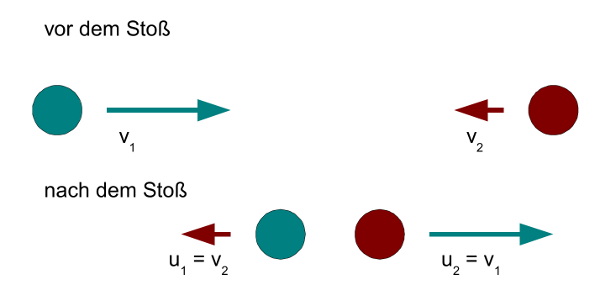
Ein Spezialfall dieses Spezialfalles ist der Fall, dass die Kugeln neben gleicher Masse auch noch
gleiche Geschwindigkeiten haben. Wobei wir mit „gleich“ hier meinen, dass die
Geschwindigkeiten denselben Betrag v1 haben. Die beiden Kugeln können nur dann
aufeinanderprallen, wenn sie sich aufeinander zu bewegen – ihre Geschwindigkeiten haben also
entgegengesetzte Richtungen. Das drückt man durch ein Minuszeichen aus. Hat die erste Kugeln
die Geschwindigkeit v1, hat die zweite Kugel also die Geschwindigkeit −v1.
Damit erhält man: u1 = −v1 und u2 = v1. Somit ist aber auch u2 = −u1.
Was hier passiert, ist also folgendes: Beide Kugeln laufen aufeinander zu, die erste von links nach
rechts mit v1, die zweite von rechts nach links mit −v1, beide also mit betragsmäßig gleicher
Geschwindigkeit v1. Nach dem Stoß hat die erste Kugel nun die Geschwindigkeit u1 = −v1, das
heißt, sie läuft nun von rechts nach links, kehrt also ihre Bewegungsrichtung um. Die zweite Kugel
kehrt ihre Bewegungsrichtung ebenfalls um, denn sie hat nun die Geschwindigkeit u2 = v1.
An den Beträgen der Geschwindigkeiten hat sich nicht geändert, die sind immer noch v1!
Prallen zwei gleich schwere Kugeln mit einer betragsmäßig gleichen Geschwindigkeit aufeinander, fliegen sie nach dem Stoß in entgegengesetzte Richtungen davon, wobei ihre Geschwindigkeiten immer noch denselben Betrag haben.
- Abb. 2 ¦ Kugeln gleicher Masse und gleicher Geschwindigkeit
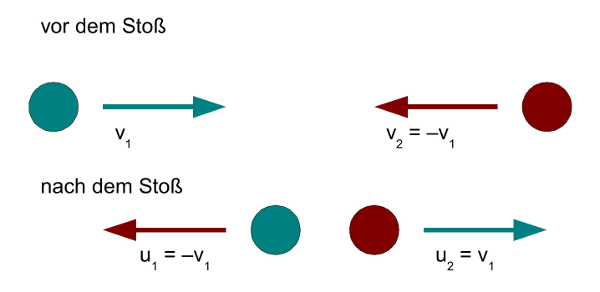
2. Eine Kugel ruht.
Die erste Kugel bewegt sich auf die zweite zu; diese ruht aber, hat also die Geschwindigkeit v2 = 0. Hier müssen wir mehrere Fälle unterscheiden:
a) Sind wieder beide Kugeln gleich schwer, ergibt sich für die Endgeschwindigkeiten aus den Gleichungen (4): u1= 0 und u2 = v1.
Wieder tauschen die beiden Kugeln die Geschwindigkeiten – die zweite bewegt sich mit der Geschwindigkeit und der Richtung der ersten Kugel vom Ort des Stoßes weg, die erste bleibt dort liegen, denn ihre Endgeschwindigkeit ist null.
- Abb. 3 ¦ Kugeln gleicher Masse, eine Kugel ruht
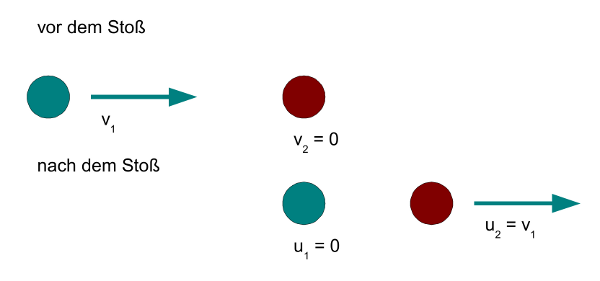
b) Haben die Kugeln unterschiedliche Massen, müssen wir wieder die komplizierteren
Gleichungen 3 nehmen. Setzt man v2 = 0 ein, erhält man:
(5) 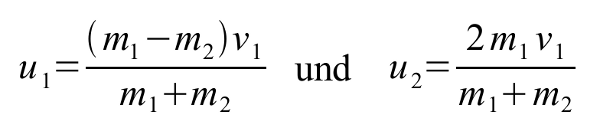
Jetzt betrachten wir anhand dieser Gleichungen 5 zwei unterschiedliche Fälle:
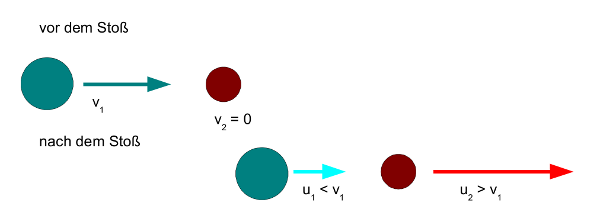
I) Die Masse der ersten Kugel ist größer als die der zweiten Kugel:
m1 > m2.
Damit wird die Differenz m1 − m2 im Bruch, der u1 beschreibt, positiv. Der Faktor 2 m1 im Bruch für u2 ist ebenfalls positiv, und die beiden Nenner sind es auch. Damit haben die
Endgeschwindigkeiten beider Kugeln dasselbe Vorzeichen und zwar dasjenige von v1 – was
bedeutet, beide Kugeln bewegen sich nach dem Stoß in dieselbe Richtung und zwar in die, in
die die erste Kugel vor dem Stoß unterwegs war. Da beide Brüche denselben Nenner haben,
hängt ihr Größenverhältnis vom Zähler ab. Während bei u1 der Faktor vor v1 kleiner ist als m1 (es
wird ja etwas von m1 subtrahiert), ist der Faktor bei u2 größer als m1 (m1 wird ja verdoppelt). Damit ist auch u2 > u1. Das bedeutet, die zweite, leichtere Kugel ist nach dem Stoß schneller als die
erste, schwerere. Während bei gleich schweren Kugeln die zweite Kugel die Geschwindigkeit der
ersten vollständig übernimmt, bekommt sie jetzt nur einen Teil ab. Die erste Kugel behält einen Teil
ihrer Geschwindigkeit und bewegt sich ebenfalls weiter, wird aber abgebremst.
Die Differenz m1 &minus m2 ist immer kleiner als die Summe m1 + m2, das bedeutet, der Quotient aus beiden in u1 ist kleiner als 1. Damit ist u1 < v1. Die erste Kugel ist also nach dem Stoß langsamer
als sie es vorher war. Das leuchtet ein, da sie ja Geschwindigkeit an die zweite abgegeben hat.
Das Produkt 2m1 ist dagegen immer größer als die Summe m1 + m2, da wir ja m1 > m2 vorausgesetzt hatten. Somit ist der Quotient dieser beiden Ausdrücke größer als 1 und u2 > v1. Damit ist die
zweite Kugel nach dem Stoß schneller als die erste vor dem Stoß war. Je geringer ihre Masse im
Vergleich zur ersten Kugel ist, desto schneller wird sie.
- Abb. 4 ¦ Masse der ersten Kugel größer
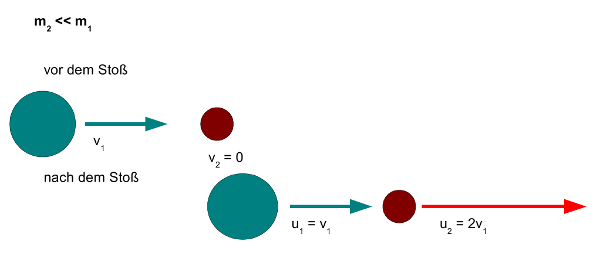
Sehen wir uns nun noch den Fall an, dass die erste Kugel sehr viel schwerer ist als die zweite
Kugel, so viel schwerer, dass die Masse m2 der zweiten Kugel gegenüber m1 vernachlässigt werden
kann. Dann kann die Differenz m1 − m2 gleich m1 gesetzt werden, die Summe m1 + m2 ist ebenfalls gleich m1. Damit wird u1 gleich v1, die erste Kugel läuft also nach dem Stoß unbeeindruckt mit ihrer alten Geschwindigkeit in der alten Richtung weiter. Da der Nenner
im Bruch ja gleich m1 ist, wird u2 gleich 2v1.
Die zweite, sehr leichte Kugel wird also mit der
doppelten Geschwindigkeit der ersten Kugel von dieser weggeschossen.
- Abb. 5 ¦ Masse der ersten Kugel sehr viel größer
II) Die Masse der ersten Kugel ist kleiner als die der zweiten Kugel:
m1 < m2.
Nun wird die Differenz m1 − m2 im Bruch, der u1 beschreibt, negativ. Der Faktor 2m1 im Bruch für u2 ist weiterhin positiv, und die beiden Nenner sind ebenfalls positiv. Damit haben die
Endgeschwindigkeiten beider Kugeln entgegengesetzte Vorzeichen. Beide fliegen also nach dem
Stoß in entgegengesetzte Richtungen davon. Die erste Kugel dreht das Vorzeichen ihrer
Geschwindigkeit um, das heißt, sie kehrt ihre Bewegungsrichtung nach dem Stoß um; die zweite
Kugel wird in Richtung von v1, also in die Richtung der ersten Kugel von vor dem Stoß, in
Bewegung gesetzt.
Die erste Kugel setzt die zweite in Bewegung, prallt aber auch selbst an der ersten ab.
Um die Größenverhältnisse der Endgeschwindigkeiten zu untersuchen, sehen wir uns wieder verschiedene Fälle an.
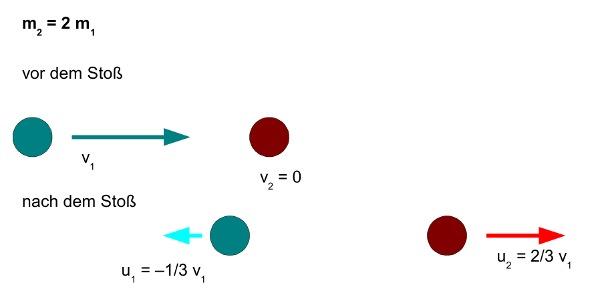
i) Die zweite Kugel ist nur wenig schwerer als die erste Kugel. Sehen wir uns zunächst noch mal Fall 2a) an: Beide Kugeln sind gleich schwer – die stoßende Kugel bleibt nach dem Stoß liegen und die angestoßene Kugel läuft mit v1 davon.
Nehmen wir als Beispiel an, die zweite Kugel hätte die Masse m2 = 2m1. Setzen wir diesen Wert in die Gleichungen 5 ein, erhalten wir u1 = −1/3 ⋅ v1 und u2 = 2/3 ⋅ v1. Die zweite, angestoßene Kugel rollt nun also mit nur noch 2/3 der Geschwindigkeit aus Fall 2a) davon, während die erste Kugel mit 1/3 des Betrages ihrer ursprünglichen Geschwindigkeit v1 in die Gegenrichtung zurückfliegt. Die erste, stoßende Kugel ist nach dem Stoß langsamer als die zweite, angestoßene Kugel und kehrt ihre Richtung um.
- Abb. 6 ¦ Zweiten Kugel doppelt so schwer
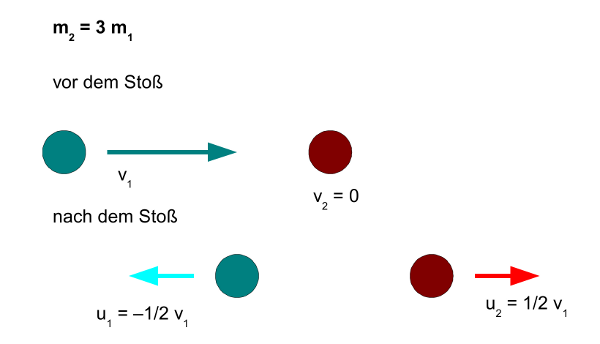
ii) Die zweite Kugel ist dreimal so schwer wie die erste Kugel, es ist also m2 = 3m1. Setzen wir diese Werte in die Gleichungen 5 ein, erhalten wir u1 = −1/2 ⋅ v1 und u2 = 1/2 ⋅ v1. Beide Kugeln sind also nach dem Stoß gleich schnell, bewegen sich aber in entgegengesetzter Richtung davon.
- Abb. 7 ¦ Zweite Kugel dreimal schwerer
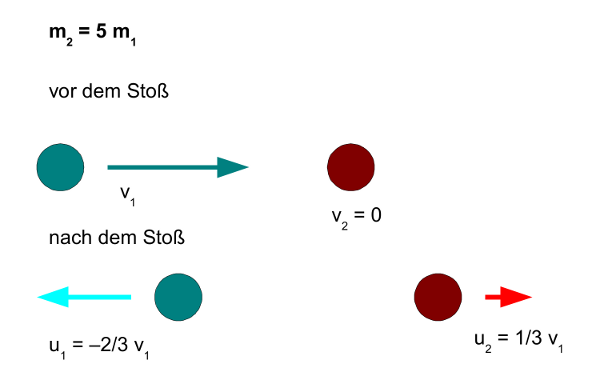
iii) Die zweite Kugel ist mehr als dreimal so schwer wie die erste Kugel. Ist sie beispielsweise fünfmal so schwer, also m2 = 5m1, ergibt sich u1 = −2/3 ⋅ v1 und u2 = 1/3 ⋅ v1. Nun ist also die Geschwindigkeit der stoßenden, ersten Kugel nach dem Stoß betragsmäßig höher als die der zweiten, angestoßenen Kugel. Je schwerer die zweite Kugel ist, desto schneller wird sie im Vergleich zur ersten, stoßenden Kugel.
- Abb. 8 ¦ Zweite Kugel fünfmal schwerer
Damit kommen wir zu Fall
iv) Die Masse der zweiten Kugel m2 soll jetzt so viel größer sein als die der ersten Kugel, dass wir
die Masse der ersten Kugel m1 vernachlässigen, also näherungsweise gleich null setzen können.
Wenn wir m1 gleich null setzen, wird aus den Gleichungen 5
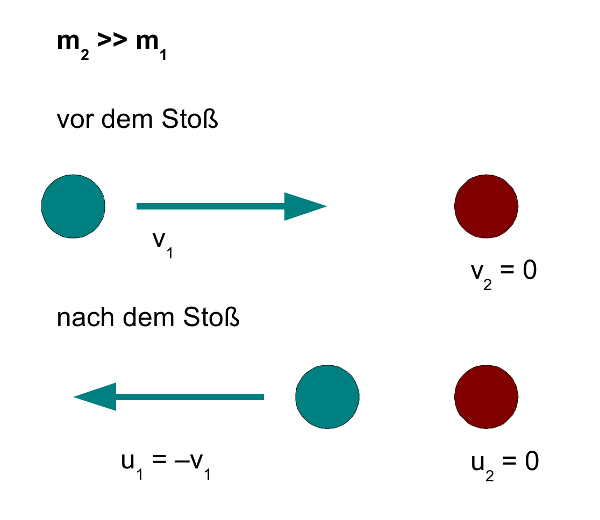
u1 = −v1 und u2 = 0.
Das heißt, die zweite, viel schwerere Kugel bleibt nach dem Stoß
unbeeindruckt dort liegen, wo sie anfangs lag, und die erste, stoßende Kugel prallt an ihr ab und
fliegt mit ihrer ursprünglichen Geschwindigkeit v1 in die Gegenrichtung zurück.
Das ist zum Beispiel der Fall, wenn die erste, stoßende Kugel gegen eine feststehende Mauer prallt
und diese an die Stelle der zweiten Kugel tritt. Da die Mauer feststeht, kann ihre Masse als
unendlich groß angenommen werden.
- Abb. 9 ¦ Zweite Kugel sehr viel schwerer
Das Newtonsche Kugelpendel
- Abb. 10 ¦ Newtonsches Kugelpendel
Lenkt man eine der gleich schweren Kugeln aus und lässt sie auf die anderen prallen, bleiben die 3 mittleren in Ruhe und die 5. auf der anderen Seite fliegt davon. Was man hier sieht, ist der Fall 2a), dass eine Kugel auf eine gleich schwere ruhende prallt und selbst zur Ruhe kommt. Nur dass die ruhende Kugel gar nicht dazukommt, selbst wegzufliegen, da sie ihrerseits sofort auf den nächsten ruhenden Nachbarn prallt und selbst zur Ruhe kommt, bevor sie ans fliegen denken konnte. Erst die äußerste Kugel auf der anderen Seite hat keinen Nachbarn maehr und fliegt mit (annähernd) derselben Geschwindigkeit davon.
- Abb. 11 ¦ Newtonsches Kugelpendel
Entsprechend fliegen gegenüber zwei Kugeln weg, wenn man zwei Kugeln auslenkt, und drei, wenn man drei auslenkt.
- Abb. 12 ¦ Newtonsches Kugelpendel
-
© Wiebke Salzmann, Juni 2012
