Dr. Wiebke Salzmann
freie Lektorin und Autorin
Wissenstexte
Physik-Wissen
Kreiselkompass

Auf dieser Seite erwartet Sie die Funktionsweise des Kreiselkompasses.
www.wissenstexte.de > Physik-Wissen > Mechanik > Kreiselkompass
Kreiselkompass
– Aufbau und Funktion des Kreiselkompasses
– Nord-Süd-Ausrichtung
– Missweisung bei Nord-Süd-Bewegungen
Ein magnetischer Kompass weist bekanntlich nicht exakt nach Norden, da die magnetischen Pole nicht genau auf den geografischen Polen liegen. Der Grund hierfür ist, dass die Achse des magnetischen Dipols, den man sich in der Erde denken kann, nicht parallel zur Drehachse der Erde gerichtet ist. Außerdem funktioniert ein magnetischer Kompass nicht richtig, wenn zu viel Metall in der Nähe ist – wenn er zum Beispiel in einem U-Boot von Metall umschlossen ist. Mit einem Kreiselkompass hat man diese Probleme nicht.
Drehimpulserhaltung
Die Funktion des Kreiselkompasses beruht auf der Impulserhaltung, genauer gesagt, auf der Drehimpulserhaltung. Jeder Körper hat einen Impuls. Das ist eine Größe, die sich aus der Masse des Körpers und seiner Geschwindigkeit zusammensetzt. Hat der Körper die Geschwindigkeit null, ruht er also, ist auch sein Impuls null.
Solange keine Kräfte auf einen Körper wirken, behält er seinen Impuls bei – der Impuls bleibt erhalten. Einmal mit einer bestimmten Geschwindigkeit in eine bestimmte Richtung in Bewegung gesetzt, wird sich ein Raumschiff daher so lange in diesem Tempo in die eingeschlagene Richtung bewegen, bis erneut eine Kraft auf es einwirkt (Impulserhaltungssatz). Auf der Erde kommen in Bewegung gesetzte Fahrzeuge in der Regel recht schnell wieder zum Stillstand – aber hier gibt es eine weitere Kraft, die das bewirkt: Die Reibungskraft bremst ein Fahrzeug ab.
Man spürt jedoch deutlich das Bestreben des (eigenen) Körpers, den Impuls beibehalten, wenn man in einem Fahrzeug sitzt und dieses bremst. Zwar wird das Fahrzeug langsamer, aber der eigene Körper bewegt sich noch in Fahrtrichtung fort, bis – je nach Geschwindigkeit und Spontaneität des Abbremsens – entweder die eigene Muskelkraft oder die nächste Wand diese Bewegung aufhält.
Auch Drehbewegungen sind mit einem Impuls verbunden – dem Drehimpuls. Für Drehbewegungen gibt es daher ebenfalls einen Erhaltungssatz, den Drehimpulserhaltungssatz: Ein sich drehender Körper möchte seinen Drehimpuls beibehalten. Das bedeutet, er möchte sowohl die Geschwindigkeit als auch die Richtung seines Drehimpulses beibehalten. Die Richtung des Drehimpulses ist so festgelegt, dass sie senkrecht auf der Drehbewegung steht und in Richtung der Drehachse zeigt. Bei einem sich drehenden Rad zeigt der Drehimpuls also in Richtung der Radachse.
Die Drehimpulserhaltung erleichtert uns übrigens das Rad fahren – da das sich drehende Rad seinen Drehimpuls beibehalten will, fällt es nicht um. Denn dadurch würde die Drehachse ihre Richtung ändern, und mit ihr auch der Drehimpuls. Damit fällt aber auch das ganze Fahrrad nicht um. Deshalb ist umso leichter, das Gleichgewicht zu halten, je schneller man fährt (je höher also der Drehimpuls des Rades ist).
Das kann man in einem einfachen Experiment veranschaulichen: Man baut das Vorderrad eines Fahrrades aus und befestigt rechts und links an der Nabe je eine Schnur. An den Schnurenden hält man das Rad hoch und lässt es von einem Helfer in Drehung versetzen. Nun kann man eine der Schnüre loslassen und das Rad bleibt aufrecht stehen. Erst wenn die Drehung langsamer wird, kippt auch das Rad. (Es kostet übrigens auch dann, wenn man den Drehimpulserhaltungssatz verstanden hat, etwas Überwindung, eine Schnur loszulassen …)
- Abb. 1 ¦ Experiment zur Drehimpulserhaltung

- Einmal in Drehung versetzt, bleibt das Rad aufrecht stehen, auch wenn es nur noch auf einer Seite von einer Schnur gehalten wird.
Aufbau und Funktion des Kreiselkompasses
Zurück zum Kreiselkompass. Die Abbildung zeigt den prinzipiellen Aufbau eines solchen Gerätes:
- Abb. 2 ¦ Kreiselkompass
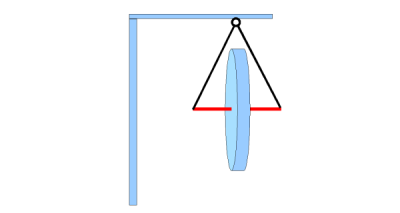
- Prinzipieller Aufbau des Kreiselkompasses
Der Kreisel (eine Scheibe) ist so aufgehängt, dass er sich um die waagerechte Drehachse (rot) drehen kann, und die Aufhängung erlaubt ebenfalls Drehungen. Wird nun eine solche Scheibe in Drehung versetzt, hat auch sie das Bestreben, diese Drehung beizubehalten.
Dabei gibt es ein Problem – die Richtung des Drehimpulses bezieht sich nämlich nicht auf die Erdoberfläche, sondern auf den physikalischen Raum, ein abstraktes Gebilde. Die Erde dreht sich nun aber selbst ebenfalls in diesem Raum. Das bedeutet, während der Kreiselkompass um eine Drehachse, die ihre Richtung im Raum nicht ändern will, rotiert, dreht sich die Erde unter ihm. (Natürlich bewegt sich der Kreisel insofern mit der Erde mit, als die Halterung auf ihr steht und er so mit ihr verbunden ist. Der Kreisel selbst ist ja aber beweglich aufgehängt, weshalb er die Richtung seiner Drehachse durch eine Auslenkung in der Aufhängung beibehalten kann; siehe hierzu die Abbildung unten.) Relativ zur Erdoberfläche ändert sich die Richtung der Drehachse des Kreisels also durchaus. Damit wäre der Kreiselkompass als solcher nicht zu gebrauchen. Dass es trotzdem funktioniert, liegt an der Eigenschaft von Kreiseln, Kräften auszuweichen. Das bewirkt nämlich eine automatische Ausrichtung des Kreisels in Nord-Süd-Richtung.
Ausrichtung des Kreisels in Nord-Süd-Richtung
Sehen wir uns nun einen solchen Kreiselkompass an, der sich am Äquator befindet.
- Abb. 3 ¦ Kreiselkompass – Funktionsweise
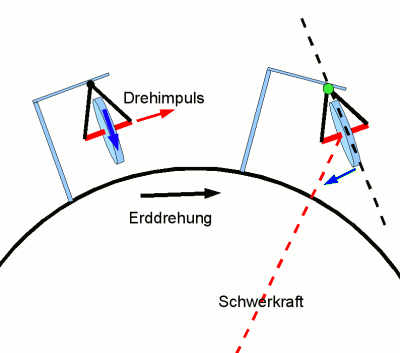
- Wirkung der Erddrehung auf einen Kreiselkompass. (Blickrichtung von Süden)
Der Kreisel dreht sich um die rote Achse. Zunächst ist diese Drehachse parallel zum Äquator ausgerichtet (links), und damit auch der Drehimpuls (roter Pfeil). Nun dreht sich die Erde (schwarzer Pfeil), weshalb die Drehachse des Kreisels nach einer Weile schräg zum Äquator steht (rechts). Vielmehr, sie würde schräg nach oben zeigen, wenn nicht die Schwerkraft (rot, gestrichelt) auf den Kreisel wirken würde. Sie greift am Schwerpunkt des Kreisels (also in seinem Mittelpunkt) an und versucht, ihn nach unten zu ziehen, um den Kreisel wieder in die Senkrechte zu bringen. Das bedeutet aber eine Drehbewegung (blauer Pfeil rechts) des Kreisels um eine Achse, die durch die Aufhängung am Balken geht und senkrecht zur Bildschirmebene gerichtet ist (der grüne Punkt ist der Durchstoßpunkt).
Auch zu dieser Drehbewegung gehört ein Drehimpuls. Er ist parallel zu der eben beschriebenen Achse, die durch den günen Punkt symbolisiert wird, und ist hier in die Zeichenebene hineingerichtet. Der Gesamtdrehimpuls des Kreisels ergibt sich nun als Summe der Drehimpulse aus der Drehung um die rote Achse und der Drehung um die grüne Achse. Drehimpulse sind Vektoren, müssen also wie solche addiert werden.
Da die Kräfte vom ersten Moment an wirken, kommt es in Wirklichkeit nicht zu einer solchen Schräglage des Kompasses wie in der letzten Abbildung. Wir können die Drehachse des Kreisels (rot) also weiterhin als parallel zur Erdoberfläche annehmen. Zu dem hierzu gehörenden Drehimpuls wird nun vektoriell der von der Schwerkraft verursachte Drehimpuls (grün) addiert (indem man also die Drehimpulse als Pfeile zeichnet und diese aneinanderhängt, um dann den Anfangspunkt des ersten mit dem Endpunkt des zweiten zu verbinden).
Der Summenpfeil (schwarz) ergibt den Gesamtdrehimpuls. Er zeigt schräg in Richtung Pol. Dies ist die Richtung, in die sich der Kreisel, genauer gesagt, seine Drehachse, einstellt. Denn die Drehachse muss ja in Richtung des neuen Gesamtdrehimpulses zeigen.
Hiermit ist aber nun nicht Schluss, die Schwerkraft wirkt ja weiterhin und bewirkt eine neuerliche Änderung des Gesamtdrehimpulses. Der Kreisel dreht sich also weiter, und zwar so lange, bis seine Drehachse genau in Nord-Süd-Richtung zeigt. Steht er erst einmal so, bleibt er auch so stehen. Denn nun führt die Erddrehung nicht mehr zu einer potenziellen Schräglage der Kreiseldrehachse, womit die Schwerkraft keine „Angriffsfläche“ mehr hat.
Statt die Nutzung des Kreisels als Kompass unmöglich zu machen, ist es also gerade die Erddrehung, die eine Ausrichtung des Kreisels in Nord-Südrichtung erzwingt.
- Abb. 4 ¦ Gesamtdrehimpuls des Kreisels
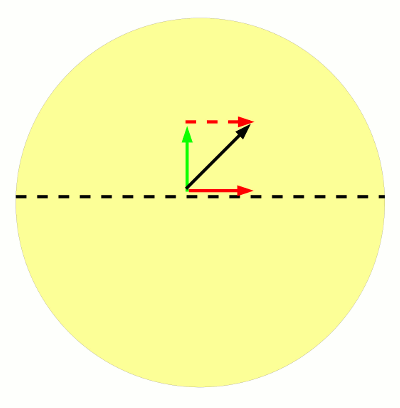
- Wir blicken nun von „vorn“ auf den Kreiselkompass und addieren die Drehimpulse. (In Abbildung 3 entspricht diese Blickrichtung derjenigen von oben.) Die gestrichelte schwarze Linie stellt den Äquator dar.
Missweisung bei Nord-Süd-Bewegungen
Streng genommen gilt das Gesagte nur bei Bewegungen in Ost-West-Richtung. Bewegt sich ein Schiff nord- oder süwärts, kommt es zu einer Missweisung des Kompasses.
Nehmen wir an, das Schiff steht zu Beginn am Äquator, die Achse des Kreisels zeigt genau nach Nord und steht somit parallel zur Erdoberfläche. Nun fährt das Schiff los in Richtung Norden. Die Achse des Kreisels möchte wieder ihre Richtung im Raum beibehalten – und das führt genau wie in Abbildung 3 gezeigt zu einer Schräglage der Achse gegenüber der Erdoberfläche (nur dass sich nun nicht die Erde unter dem Kompass dreht, sondern der Kompass sich nach Norden bewegt). Auch diesmal greift die Gravitation an und will die Kreiselachse wieder in die Waagerechte bringen. Der Kreisel weicht wieder aus und die Achse zeigt deshalb nicht mehr genau nach Norden, sondern in eine Richtung, die sich aus der Bewegung des Schiffes und der Geschwindigkeit der Erddrehung (an der Erdoberfläche 1600 km/h) ergibt. Solange das Schiff deutlich langsamer ist als die Erddrehung schnell ist, ist die Abweichung nur gering.
An den Polen funktionieren übrigens beide Kompasse nicht – der magnetische, weil sich hier die Abweichungen von magnetischem und geografischem Pol viel zu stark bemerkbar machen; der Kreiselkompass, weil die Erdachse hier senkrecht aus dem Boden kommt und damit parallel zur Gravitation gerichtet ist. Der Kreisel hängt am Pol also immer senkrecht nach unten und die Erddrehung hat deshalb hier keinen Einfluss auf die Drehachse des Kreisels.
© Wiebke Salzmann, November 2008
