Inkohärentes Licht

Das von einer gewöhnlichen Lichtquelle ausgesandte Licht setzt sich aus vielen einzelnen Wellenzügen zusammen. Bei natürlichen Lichtquellen sind diese Wellenzüge nicht kohärent – natürlich ausgestrahltes Licht ist inkohärent. Das versteht man, wenn man sich überlegt, dass die eigentlichen Lichtquellen Atome sind. Die Ausstrahlung eines einzelnen Wellenzuges bei einem Emissionsvorgang dauert etwa 0,000 000 000 1 s, daraus ergibt sich eine theoretische Länge eines solchen ausgesandten Wellenzuges von etwa 3 cm.
Betrachten wir nun ein solches Atom, das einen Wellenzug aussendet, und stellen uns neben den Lichtweg. Der erste Wellenzug zieht an uns vorbei. Irgendwann sendet das Atom den nächsten Wellenzug aus, und zwar zu einer zufälligen späteren Zeit. Die Berge und Täler dieses zweiten Wellenzuges stehen zu denen des ersten in einer zwar festen, aber völlig willkürlichen Phasenbeziehung. Dasselbe gilt für den dritten, vierten, fünften … Wellenzug. Zwischen den einzelnen vom Atom ausgesandten Wellenzügen ist daher keine feste Phasenbeziehung feststellbar – von Wellenzug zu Wellenzug wechselt sie ständig. Eine feste Phasenbeziehung kann nur zwischen zwei einzelnen Wellenzügen auftreten, also maximal über die Länge eines solchen Wellenzuges. Je kürzer diese sind, desto kürzer die Strecke, über die es zu Kohärenz kommen kann (die Kohärenzlänge).
Selbst wenn die Wellenzüge sehr lang sind, kommt noch hinzu, dass eine gewöhnliche Lichtquelle Licht verschiedener Wellenlängen aussendet. Zwischen zwei Wellenzügen unterschiedlicher Wellenlänge ändert sich die Phasendifferenz entlang der Wellenzüge ebenfalls (Abbildung 2b). (Kurz kann ein Wellenzug auch nur dann sein, wenn er aus Wellen vieler Frequenzen zusammengesetzt ist. Je länger er ist, desto weniger Frequenzen sind beteiligt, desto reiner ist seine Farbe.)
Schließlich sendet eine gewöhnliche Taschenlampe auch kein paralleles Licht aus, sondern in alle möglichen Richtungen.
Eine gewöhnliche Taschenlampe (Abbildung 1) sendet also inkohärentes Licht aus. Sie stellt eine ausgedehnte Lichtquelle dar, deren Atome kurze Wellenzüge in alle möglichen Richtungen aussenden. Weder entlang der Ausbreitungsrichtung (Pfeil) noch senkrecht zu ihr (gestrichelte Linie) finden sich feste Phasenbeziehungen zwischen den Wellen.

  Abb. 1 ¦ Inkohärentes Licht  

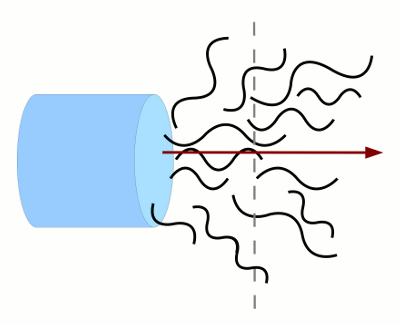
Bildunterschrift Inkohärentes Licht einer Taschenlampe: Die Wellenzüge breiten sich in alle möglichen Richtungen aus (das Licht ist nicht parallel); die Wellenzüge sind kurz und haben verschiedene Wellenlängen (das Licht ist nicht monochromatisch).Bildunterschrift Ende

Räumlich kohärentes Licht

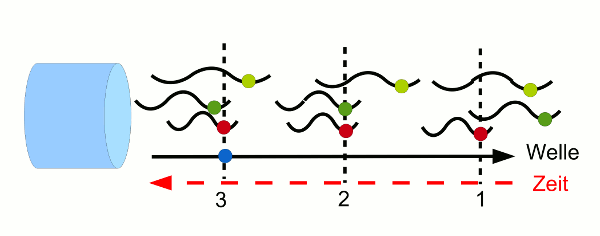
Betrachten wir eine Taschenlampe, die drei Atome enthält. Jedes dieser drei Atome sendet kurze Wellenzüge aus, jedes in einer anderen Wellenlänge und jedes zu zufällig verteilten Zeiten. Wichtig ist, dass die Lampe nur nach vorn strahlen soll, die Wellenzüge sind also alle parallel zueinander. (Was es bedeutet, wenn sie nicht parallel sind, siehe weiter unten.) Stellt man sich an den Strahl der Taschenlampe (Abbildung 2a) an den blauen Punkt, laufen verschiedenste Kombinationen aus Wellenzügen an einem vorbei. Das erste Minimum des untersten wählen wir als Referenz (rote Punkte). Die Lage der ersten Minima der Wellenzüge des mittleren und oberen Atoms gibt dann die Phasenverschiebungen dieser Wellenzüge zum unteren wieder (grüne Punkte).
In Abbildung 2a sind nun drei Zeitpunkte skizziert. Da die Wellen sich nach rechts ausbreiten, sieht man zuerst den mit 1 gekennzeichneten Zustand, zuletzt den mit 3 gekennzeichneten. Man sieht – die Phasenverschiebungen zwischen den Wellenzügen der drei Atome wechseln (aus der Sicht des blauen Punktes) ständig. Das Licht dieser Taschenlampe ist also nicht zeitlich kohärent.
Setzt man sich aber auf einen der Wellenzüge (also beispielsweise auf einen der roten Punkte), bewegt sich mit ihm mit und schaut senkrecht zur Ausbreitung, sieht man immer dieselbe Phasenverschiebung zu den anderen beiden Wellenzügen. Innerhalb einer einzigen solchen Gruppierung von Wellenzügen bleibt die Phasenverschiebung während der Lichtausbreitung also erhalten – parallele Wellen sind räumlich kohärent.

  Abb. 2a ¦ Räumlich kohärentes Licht  

Bildunterschrift Die Wellenzüge breiten sich parallel aus, und zwar entlang des schwarzen Pfeils nach rechts. Ein am blauen Punkt stehender Beobachter sieht nacheinander die Zustände 1, 2, 3 an sich vorüberziehen (die Zeitachse zeigt deshalb nach links).
Zwischen zeitlich aufeinanderfolgenden Gruppierungen von Wellenzügen ändert sich die Phasenbeziehung ständig, zeitliche Kohärenz liegt daher nicht vor.
Die Phasenbeziehung zwischen zwei oder mehreren Wellenzügen innerhalb einer bestimmten Gruppierung von Wellenzügen bleibt während der Ausbreitung jedoch erhalten; senkrecht zur Ausbreitungsrichtung gibt es also feste Phasenbeziehungen: Das Licht ist rämlich kohärent.
(Die Wellenzüge müssen natürlich nicht so klar voneinander getrennte Gruppen bilden. Das soll nur die Darstellung übersichtlicher machen).Bildunterschrift Ende

  Abb. 2b ¦ Räumlich kohärentes Licht  

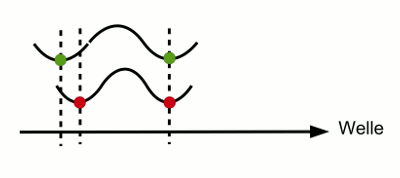
Bildunterschrift Hier ist noch einmal verdeutlicht, wie sich die unterschiedlichen Wellenlängen auswirken: Während die ersten Minima beider Wellenzüge in Phase sind, besteht zwischen den zweiten ein Phasenunterschied, da der obere Wellenzug eine größere Wellenlänge hat. Entlang der Welle bleibt der Phasenunterschied zwischen beiden also nicht konstant. Licht aus mehreren Wellenlängen – also aus mehreren Farben – ist also nicht zeitlich kohärent. Sofern die Wellen sich parallel ausbreiten, ist es aber rämlich kohärent.Bildunterschrift Ende

Zeitlich kohärentes Licht

Licht einer einzigen Frequenz bildet einen unendlich langen Wellenzug. Solches Licht nennt man monochromatisch – da „eine Frequenz“ gleichbedeutend ist mit „eine Farbe“. Stellt man sich neben eine monochromatische Welle, die aus mehreren Wellenzügen besteht, werden sich die Phasenbeziehungen zwischen all diesen Wellenzügen nicht ändern. Da alle dieselbe Frequenz haben, kommt es zu keinen Verschiebungen zwischen ihnen und da sie unendlich lang sind, tritt auch der Fall nicht auf, dass nachfolgende Wellen eine andere Phase haben und dadurch einen „Bruch“ in der Phasenbeziehung auslösen. Monochromatisches Licht ist also zeitlich kohärent (hat eine unendliche Kohärenzlänge). Stellt man sich in Abbildung 3 beispielsweise an den mit 2 bezeichneten Ort und sieht den Wellen beim Vorbeiziehen zu, wird während der ganzen Zeit, in der der unendliche lange Wellenzug vorbeizieht, die Phasenverschiebung zwischen dem untersten und dem obersten Wellenzug eine knappe Wellenlänge betragen. Die Wellenzüge haben also längs ihrer Ausbreitungsrichtung eine feste Phasenverschiebung – und zwar aufgrund des unendlich langen Wellenzuges „auf immer und ewig“ (Abbildung 3b).

Senkrecht zur Ausbreitungsrichtung kann es dagegen durchaus zu Änderungen der Phasenbeziehung kommen, wenn die Wellenzüge beispielsweise in unterschiedlichen Winkeln ausgesandt werden – wie es in dem sich aufweitenden Strahl einer Taschenlampe der Fall ist. Alle Wellenzüge verlassen die Lampe zum Zeitpunkt 1 mit derselben Phase (hier: Nulldurchgang vom Maximum zum Minimum), gekennzeichnet durch die roten Punkte in Abbildung 3b. Setzen wir uns zum Zeitpunkt 1 auf die Welle und zwar auf den roten Punkt der untersten Welle und fliegen mit der Welle mit. Zum Zeitpunkt 2 haben sich alle Wellenzüge um die Entfernung von zwei Wellenlängen nach rechts bewegt (und wir mit). Weil die beiden oberen Wellen sich aber in einem Winkel zum unteren ausbreiten, befinden sich deren entsprechende Nulldurchgänge nicht mehr auf einer Höhe mit dem der unteren Welle (blaue Punkte), sie hinken hinterher (um im Bild zu bleiben: Wir müssen nun nicht mehr nach links gucken, um sie zu sehen, sondern uns nach hinten umdrehen): Eine Phasendifferenz ist entstanden. Diese Phasendifferenz wird mit weiterem Fortschreiten der Welle immer größer (grüne Punkte). Räumliche Kohärenz herrscht hier also nicht (oder bestenfalls nur über Ausschnitte des Strahls, die so eng sind, dass die Aufweitung vernachlässigbar ist).

  Abb. 3a ¦ Zeitlich kohärentes Licht  

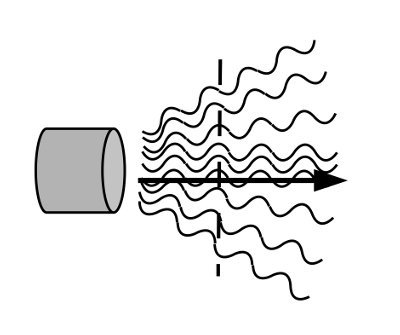
Bildunterschrift Zeitlich kohärentes Licht einer „monochromatischen Taschenlampe“.
Die ausgesandten Lichtwellen sind monochromatisch, also unendlich lang; es herrscht zeitliche Kohärenz. Sie werden aber in einem aufgefächerten Bündel ausgesandt, die Wellenzüge sind also nicht parallel zueinander. Sucht man sich einen heraus, um dessen Ausbreitungsrichtung als Ausbreitungsrichtung des Lichtes festzulegen (hier: den in der Mitte; Pfeil), stellt man fest, dass senkrecht zu dieser Ausbreitungsrichtung die Phasendifferenz nicht erhalten bleibt (gestrichelte Linie). Das Licht ist räumlich also nicht kohärent.Bildunterschrift Ende

  Abb. 3b ¦ Zeitlich kohärentes Licht  

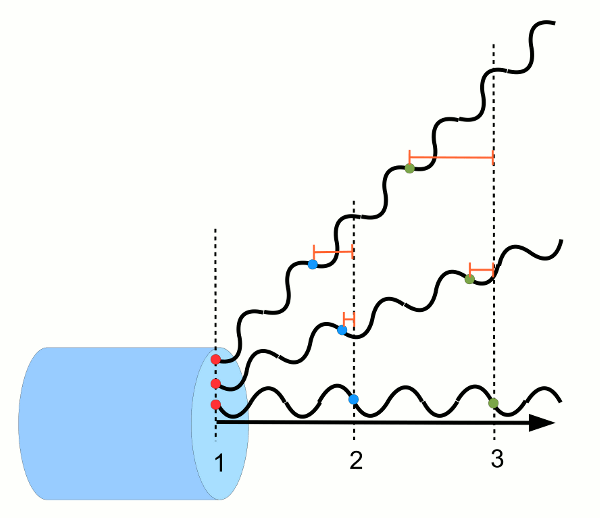
Bildunterschrift Hier ist noch einmal genauer gezeigt, wieso das Licht einer „monochromatischen Taschenlampe“ nicht räumlich kohärent ist. Alle Wellenzüge verlassen die Lampe zum Zeitpunkt 1 mit derselben Phase (hier: Nulldurchgang vom Maximum zum Minimum), gekennzeichnet durch die roten Punkte. Nun nehmen wir den Wellenzug, der sich genau horizontal ausbreitet, setzen uns darauf und bewegen uns mit diesem nach rechts mit. Zum Zeitpunkt 2 haben sich alle Wellenzüge um die Entfernung von zwei Wellenlängen nach rechts bewegt. Weil die beiden oberen sich aber in einem Winkel zum unteren ausbreiten, befinden sich deren entsprechende Nulldurchgänge nicht mehr auf einer Höhe mit dem der unteren Welle (blaue Punkte), sie hinken hinterher, eine Phasendifferenz ist entstanden. Diese Phasendifferenz wird mit weiterem Fortschreiten der Welle immer größer (Zeitpunkt 3, grüne Punkte).Bildunterschrift Ende

Zeitlich und räumlich kohärentes Licht

Zeitliche Kohärenz wird also durch Monochromasie erzeugt, räumliche Kohärenz entsteht, wenn die Wellenzüge alle parallel sind.
Parallele Wellen haben ebene Wellenfronten – das lässt sich leicht einsehen, wenn man die Maxima der Laserlichtwellen (Abbildung 4) miteinander verbindet und zum Vergleich dazu die Maxima der Lichtwellen der „monochromatischen Taschenlampe“ (Abbildung 3). Hier krümmen sich die Wellenfronten. Nur über kurze Abstände quer zum Strahl kann man die Wellenfront als annähernd eben betrachten und die Wellen entsprechend als parallel. Je länger die Strecke (senkrecht zum Strahl) ist, über die die Wellen genügend parallel sind, desto größer ist die räumliche Kohärenz.
Abbildung 4 schließlich zeigt Wellen, die sowohl zeitlich als auch räumlich kohärent sind: monochromatisches und paralleles Licht, wie es zum Beispiel ein Laser aussendet. Sowohl in Ausbreitungsrichtung als auch senkrecht dazu gibt es feste Phasenbeziehungen. Deshalb lassen sich mit Laserlicht die besten Interferenzerscheinungen erzeugen. (Zwar erzeugt auch ein Laser keine wirklich unendlich langen Wellenzüge, aber sie sind mit Längen von einigen Kilometern hinreichend „unendlich lang“.)

  Abb. 4 ¦ Zeitlich und räumlich kohärentes Licht  

Bildunterschrift Zeitlich und räumlich kohärentes Licht eines Lasers, der monochromatisches und paralleles Licht aussendet. Bildunterschrift Ende

  Abb. 5 ¦ Laserstrahl  

Bildunterschrift Licht eines Laser-Pointers, sichtbar gemacht in Wasser mit ein paar Tropfen Milch.Bildunterschrift Ende

  Abb. 6 ¦ Laserstrahl  

Bildunterschrift Licht eines Laser-Pointers bei „Nacht und Nebel“ im Garten.
Den Nebel braucht man, um den Strahl zur Seite hin sichtbar zu machen. Die Wassertröpfchen streuen Teile des Laserlichtes zur Seite (im Bild oben sind es die Milchtröpfchen). Sollten Sie sich selbst davon überzeugen wollen, achten Sie unbedingt darauf, dass Sie niemanden mit dem Laserstrahl blenden, Laserlicht kann Augenschäden verursachen.Bildunterschrift Ende

Bitte beachten: Niemals direkt in einen Laser hineinsehen! Es besteht die Gefahr ernsthafter Augenschäden!

Die Länge, über die zwei Wellenzüge kohärent sind, bezeichnet man als Kohärenzlänge. Genau genommen ist natürlich jedes Licht über seine Kohärenzlänge zeitlich kohärent. Beobachtbare Interferenzerscheinungen gibt es aber nur, wenn die Kohärenzlänge groß genug ist. Streng monochromatisches Licht hat eine unendlich große Kohärenzlänge, das von einem Atom ausgesandte Licht eine in der Größenordnung von 1 m, gewöhnliches Lampenlicht von nur etwa 100 μm.

Räumliche Kohärenz kann man erreichen, indem man eine annähernd punktförmige Lichtquelle verwendet. Punktförmige Lichtquellen senden kugelförmige Lichtwellen aus. Je größer die Entfernung zur Lichtquelle ist, desto flacher ist die Krümmung der Wellenfront. In genügend großer Entfernung kann man die Wellenfront als eben und das Licht als parallel betrachten – man kann zeigen, dass dann die Phasenunterschiede zwischen den Wellen verschiedener Atome der Lichtquelle keine Rolle mehr spielen. (Man muss also entweder eine sehr kleine Lichquelle verwenden oder entsprechend weit von ihr entfernt sein.) Schneidet man aus diesem parallelen Wellenbündel zwei enge Wellenbündel aus, sind diese (genügend) räumlich kohärent. Benutzt man nun noch eine monochromatische Lichtquelle, hat man gute Voraussetzungen geschaffen, um Interferenzeffekte beobachten zu können.
Ganz so ideal müssen die Bedingungen zum Glück nicht immer sein – so ist selbst beim Mondlicht die Kohärenzbedingung gut genug erfüllt, um die Koronen um den Mond zu erzeugen.